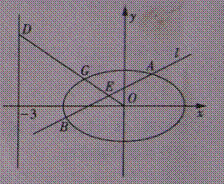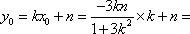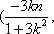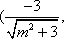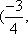- 直线与圆锥曲线的位置关系
- 共218题
请你谈一谈对“不同生产方式以及生产工艺中,生产物流管理所采用的方法和手段是不同的。”这句话的理解。
正确答案
测试
过点C(0,1)的椭圆



(1)当直线l过椭圆右焦点时,求线段CD的长;
(2)当点P异于点B时,求证:
正确答案
见解析
解析
(1)由已知得


椭圆的右焦点为







故
(2)当直线

设直线


解得


所以D点的坐标为
又直线AC的方程为

因此

所以
故
知识点
在平面直角坐标系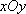
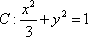
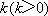
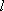
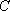

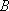
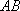
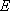

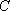
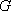
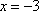

(1)求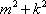
(2)若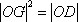
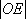
(i)求证:直线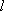
(ii)试问点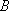

正确答案
见解析。
解析
(1)由题意:设直线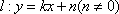
由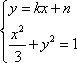
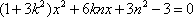
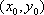
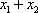
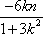
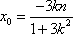
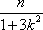
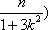
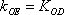
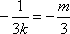
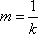

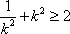
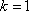
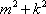
(2)(i)证明:由题意知:n>0,因为直线OD的方程为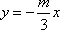
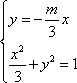
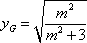
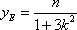
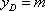


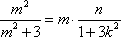
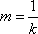
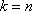
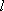
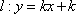
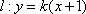
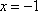
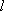
(ii)假设点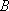


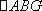
由(i)知点G(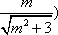
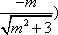
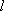
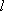
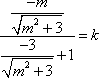
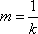
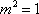
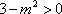

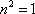
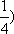
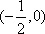
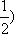
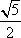
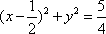

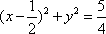
知识点
已知椭圆

(1)求椭圆C的方程;
(2)设















正确答案
见解析
解析
(1)因为椭圆过点





(2)
由题意,各点的坐标如上图所示,
则
化简得
又
所以
求得最后
所以直线
知识点
在平面直角坐标系

(1)求椭圆C的方程
(2)A,B为椭圆C上满足



正确答案
见解析。
解析
知识点
已知






(1)求圆
(2)设过点





正确答案
(1) 
(2)
解析
(1)先求圆C关于直线x + y – 2 = 0对称的圆D,由题知圆D的直径为


(2)由(Ⅰ)知
圆C:


由椭圆的焦半径公式得:

所以当
知识点
如图,动点






(1)求轨迹
(2)设直线






正确答案
(1)C的方程为4x2-y2-4=0(x≠1且x≠-1)
(2)
解析
(1)设M的坐标为(x,y),当x=-1时,直线MA的斜率不存在;当x=1时,直线MB的斜率不存在。
于是x≠1且x≠-1.此时,MA的斜率为

由题意,有

化简可得,4x2-y2-4=0
故动点M的轨迹C的方程为4x2-y2-4=0(x≠1且x≠-1)
(2)由
对于方程(﹡),其判别式
而当1或-1为方程(*)的根时,m的值为-1或1.
结合题设(m>0)可知,m>0,且m≠1
设Q、R的坐标分别为(XQ,YQ),(XR,YR),则为方程(*)的两根.
因为

所以
此时
所以
所以
综上所述,
知识点
已知椭圆C:
(1)求椭圆C的离心率;
(2)设O为原点,若点A在直线

正确答案
(1)
(2)

解析
(1)由题意,椭圆

所以


因此



(2)设点




因为
所以
即

又

因为


故线段

知识点
16.设函数
正确答案
2
解析


设



∵



∴

知识点
设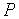
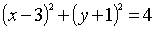
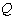
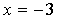
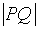
正确答案
解析
∵由圆(x-3)2+(y+1)2=4知,圆心的坐标为(3,-1),半径r=2,
∴圆心到直线x=-3的距离d=|3-(-3)|=6.
∴|PQ|min=d-r=6-2=4,故选B。
知识点
扫码查看完整答案与解析