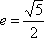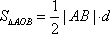- 直线与圆锥曲线的位置关系
- 共218题
设直线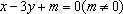
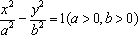
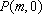
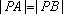
正确答案
解析
由双曲线的方程数知,其渐近线方程为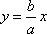
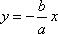
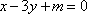
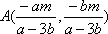
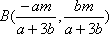
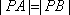
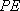
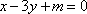
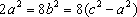

知识点
如图,在抛物线











(1)若点

(2)若

正确答案
见解析
解析
本小题主要考查抛物线的方程、圆的方程与性质、直线与圆的位置关系等基础知识,考查运算求解能力、推理论证能力,考查函数与方程思想、数形结合思想、化归与转化思想,满分12分。
(1)抛物线


由点


所以点



所以
(2)设


即
由
设

由
所以

所以圆心

从而


知识点
直线y=kx+m(m≠0)与椭圆W:
(1)当点B的坐标为(0,1),且四边形OABC为菱形时,求AC的长;
(2)当点B在W上且不是W的顶点时,证明:四边形OABC不可能为菱形。
正确答案
见解析
解析
(1)因为四边形OABC为菱形,所以AC与OB相互垂直平分。
所以可设A


所以|AC|=
(2)假设四边形OABC为菱形。
因为点B不是W的顶点,且AC⊥OB,所以k≠0.
由
设A(x1,y1),C(x2,y2),
则

所以AC的中点为M
因为M为AC和OB的交点,且m≠0,k≠0,所以直线OB的斜率为
因为k·
所以四边形OABC不是菱形,与假设矛盾。
所以当点B不是W的顶点时,四边形OABC不可能是菱形。
知识点
已知椭圆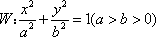

(1)求椭圆W的方程.
(2)设斜率为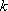
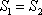
正确答案
见解析
解析
(1)解:由题意,得椭圆W的半焦距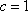
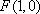
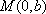
所以直线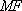
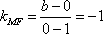
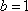
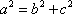
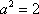
所以椭圆W的方程为
(2)证明:设直线l的方程为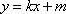
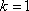
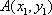
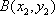
由方程组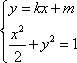
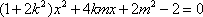
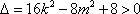
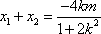
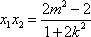
所以 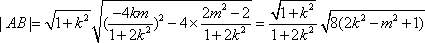
因为原点
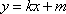
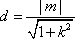
所以 
当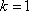
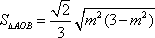
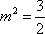
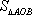
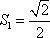
当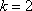
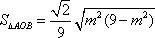


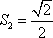
所以 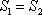
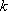
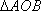
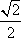
知识点
已知













(1)证明:点

(2)设点






正确答案
见解析。
解析
(1)




设
则
由题意得
所以点

经验证点




(2)由




设





由①、②得







故 
又 

所以 
由此知





(2)法二:
同理
所以
因此A、P、B、Q四点在同一圆上。
知识点
已知


(1)若
(2)求
正确答案
(1)

解析
(1)解:由题意知焦点
设



由

(2)解:设直线

由
于是
所以

由
所以

由
又因为
点

所以
记
令
可得



又
所以,当


所以,
知识点
O为坐标原点,F为抛物线C:y2=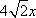
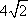
正确答案
解析
利用|PF|=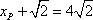
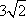
∴yP=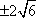

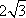
故选C.
知识点
如图,动圆C1:x2+y2=t2,1<t<3,与椭圆C2:
(1)当t为何值时,矩形ABCD的面积取得最大值?并求出其最大面积;
(2)求直线AA1与直线A2B交点M的轨迹方程。
正确答案
(1) 

解析
(1)设A(x0,y0),则矩形ABCD的面积S=4|x0||y0|。
由

x02y02=x02(1-

当


(2)由A(x0,y0),B(x0,-y0),A1(-3,0),A2(3,0)知
直线AA1的方程为
y=
直线A2B的方程为
y=
由①②得
y2=
又点A(x0,y0)在椭圆C上,故
y02=1-
将④代入③得
因此点M的轨迹方程为
知识点
椭圆






正确答案
解析
本题考查的是圆锥曲线的离心率,由题意可知,




知识点
已知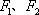
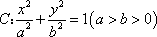
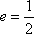
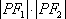
(1)求椭圆C的标准方程;
(2)过右焦点F2作斜率为k的直线l与椭圆C交于M、N两点,在x轴上是否存在点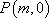
正确答案
见解析。
解析
知识点
扫码查看完整答案与解析