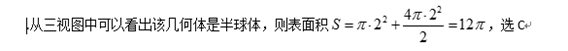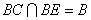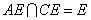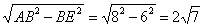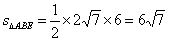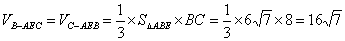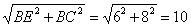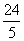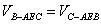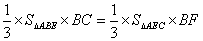- 立体几何与空间向量
- 共2637题
一简单组合体的三视图如图（2）所示，则该组合体的
体积为
A
B
C
D
正确答案
解析
由三视图知，此组合体为一个长为4，宽为3，高为1的长方体、中心去除一个半径为1的圆柱，故其体积为
知识点
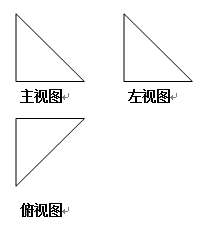
某几何体的正视图和侧视图均如图1所示，则该几何体的俯视图不可能是（ ）
A
B
C
D
正确答案
解析
略
知识点
在过正方体AC1的8个顶点中的3个顶点的平面中，能与三条棱CD 、A1D1、 BB1所成的角均相等的平面共有（ ）
正确答案
解析
略
知识点
已知几何体由正方体和直三棱柱组成，其三视图和直观图(单位：cm)如图所示.设两条异面直线
正确答案
解析
（解释性理解水平、探究性理解水平/几何体的三视图，余弦定理，异面直线所成角）由
故
由题设知
取
由余弦定理，得
知识点
一个圆柱和一个圆锥的底面直径和它们的高都与某一个球的直径相等，这时圆柱、圆锥、球的体积之比为 .
正确答案
解析
设底面半径为
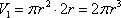
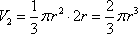
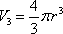
知识点
右图是一个几何体的三视图，根据图中数据，
可得该几何体的表面积是（ ）
A
B
C
D
正确答案
解析
知识点
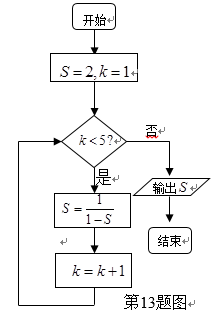
执行如右图的程序框图，那么输出
正确答案
-1
解析
第1次循环，S=﹣1，K=2，
第2次循环，S=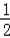
第3次循环，S=2，K=4，
第4次循环，S=﹣1，K=5，
…
框图的作用是求周期为3的数列，输出S的值，
不满足k＜5，退出循环，循环次数是4次，即输出的结果为﹣1，
故答案为：﹣1。
知识点
一个几何体的三视图如右图所示，则该几何体的表面积为 ；
正确答案
2π+24
解析
略。
知识点
已知一棱锥的三视图如图2所示，其中侧视图和俯视图都是等腰直角三角形，正视图为直角梯形，则该棱锥的体积为
正确答案
解析
该几何体是底面为直角梯形的四棱锥，依题意得
知识点
如图，一个空间几何体的主视图、左视图、俯视图为全等的等腰直角三角形，如果直角三角形的直角边长为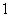
个几何体的体积为 ( )
A
B
C
D
正确答案
解析
由三视图还原几何体可知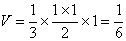
知识点
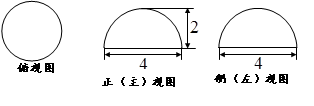
某个几何体的三视图如右上图（其中正视图中的圆
弧是半圆）所示,则该几何体的表面积为
A
B
C
D
正确答案
解析
三视图表示的几何体是由长方体和“半圆柱”组成的几何体，其中，长方体的上底面与“半圆柱”轴截面重合. 
知识点
三棱柱的侧棱与底而垂直，且底面是边长为2的等边三角形，其正(主)视图(如图所示)的面积为8，则侧(左)视图的面积为
A8
B4
C4
D
正确答案
解析
略
知识点
如图所示，一个空间几何体的正视图和左视图都是边长为
A
B
C
D
正确答案
解析
略
知识点
如图，正方形ABCD的边长为8，以ABCD为轴截面的圆柱体中，E为上底
面圆周上一点，BE=6，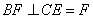
（1）求证：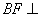
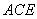
（2）求三棱锥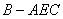
（3）求三角形AEC的面积。
正确答案
见解析。
解析
(1)证明：因为正方形ABCD为圆柱的轴截面，
所以AB为上底面圆直径
所以
因为正方形ABCD为圆柱的轴截面，
所以母线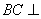
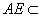
所以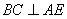
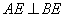
所以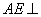
又BF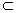
所以
所以
（2）解：在直角三角形ABE中，AB=8，BE=6，
所以AE=
母线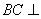
所以
（3）在三角形BCE中，BC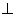
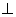
所以CE=
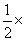
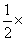
所以BF=
又
所以
所以
知识点
圆柱的侧面展开图是面积为16的正方形，则它的体积为______________________
正确答案
解析
略
知识点
扫码查看完整答案与解析