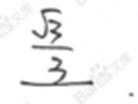立体几何与空间向量_章节学习

1

题型：单选题

|

单选题 · 5 分

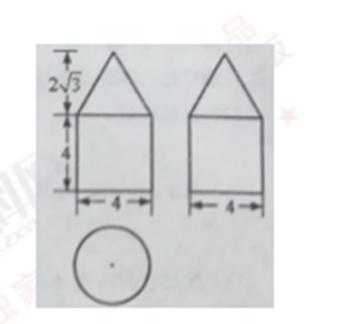
7.如图是由圆柱与圆锥组合而成的几何体的三视图，则该几何体的表面积为(　　)

A20π

B24π

C28π

D32π

正确答案

C

知识点

由三视图还原实物图空间几何体的直观图

1

题型：填空题

|

填空题 · 5 分

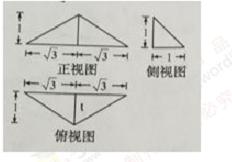
12.已知某三菱锥的三视图如图所示，

则该三菱锥的体积。

正确答案

知识点

简单空间图形的三视图由三视图还原实物图

1

题型：填空题

|

填空题 · 5 分

已知某三菱锥的三视图如图所示，则该三菱锥的体积。

正确答案

知识点

由三视图还原实物图

1

题型：填空题

|

填空题 · 5 分

10.一个几何体的三视图如图所示（单位:m）,则该几何体的体积为 .

正确答案

解析

该几何体是由两个高为1的圆锥与一个高为2的圆柱组合而成,所以该几何体的体积为 .

考查方向

本题主要考查三视图及几何体体积的计算

解题思路

由于三视图能有效的考查学生的空间想象能力,所以以三视图为载体的立体几何题基本上是高考每年必考内容,高考试题中三视图一般常与几何体的表面积与体积交汇.由三视图还原出原几何体,是解决此类问题的关键.

易错点

根据三视图得到组合体的空间结构

知识点

由三视图还原实物图

1

题型：单选题

|

单选题 · 5 分

10.某工件的三视图如图3所示，现将该工件通过切削，加工成一个体积尽可能大的正方体新工件，并使新工件的一个面落在原工件的一个面内，则原工件的材料利用率为（材料利用率=）

A

B

C

D

正确答案

A

解析

分析题意可知，问题等价于圆锥的内接长方体的体积的最大值，设长方体体的长、宽、高分别为x 、y、h，长方体上底面截圆锥的截面半径为a,则x2+y2=(2a)2=4a2,如下图所示，则可以，而长方体的体积，当且仅当时，等号成立，此时利用率为，故选A。

考查方向

本题主要考察圆锥的内接长方体和基本不等式求最值等知识，意在考察考生的空间想象能力和转化与划归的能力。

解题思路

1.先根据三视图得到原来的几何体为圆锥，后得到x2+y2=(2a)2=4a2,2.然后将长方体的体积表示为关于a的函数后利用基本不等式求最值即可。

易错点

1.找不到题中给出的关系式 x2+y2=(2a)2=4a2；2.不会利用基本不等式求最值。

知识点

由三视图还原实物图

1

题型：单选题

|

单选题 · 5 分

6. 一个几何体的三视图如图所示，则该几何体外接球的表面积为(　　)

A．

B．

C．

D．

正确答案

A

解析

由三视图可知该几何体为如图所示的三棱锥P-ABC，易知其外接圆的圆心为PC的中点O，半径，所以表面积为。

考查方向

空间几何体的三视图。

解题思路

由三视图还原出直观图是一个三棱锥，然后求出外接球的半径再进一步计算出其表面积。

易错点

不能想象出直观图是一个什么图形。

知识点

由三视图还原实物图

1

题型：单选题

|

单选题 · 5 分

10.如图，网格纸上小正方形的边长为1，粗实现画出的是某多面体的三视图，则该多面体的表面积为

A

B

C90

D81

正确答案

B

解析

由三视图该几何体是以侧视图为底面的斜四棱柱，所以该几何体的表面积

，故选B．

考查方向

本题主要考查了空间几何体的三视图及表面积等知识，为高考题的必考题，在近几年的各省高考题出现的频率较高

解题思路

三视图该几何体是以侧视图为底面的斜四棱柱，该几何体的表面积即可求出

易错点

对空间几何体的三视图及表面积理解出现错误、计算错误

知识点

由三视图还原实物图

1

题型：单选题

|

单选题 · 5 分

3．若一个几何体的三视图如图所示，这个几何体可能是一个（）

A棱台

B棱锥

C棱柱

D圆柱

正确答案

A

解析

解析已在路上飞奔，马上就到！

知识点

棱台的结构特征由三视图还原实物图

1

题型：单选题

|

单选题 · 5 分

10.某几何体的三视图如右图所示，则其体积为

A8

B

C9

D

正确答案

A

解析

由三视图可知，该几何体是有一个底面半径为1，高为5的圆柱和一个底面半径为1，高为3的圆柱的组合体，所以其体积为，故选A。

考查方向

本题主要考查三视图与几何体的结构、几何体的体积计算，意在考查考生的空间想象能力、分析转化能力与运算求解能力。

解题思路

1.先由题中给出的三视图判断出其直观图；

2.利用图中给出的数据求出该几何体的体积

易错点

1.空间想象能力较弱，无法正确判断出其直观图的形状；

2.对于几何体的体积切割不当导致出错。

知识点

组合几何体的面积、体积问题简单空间图形的三视图由三视图还原实物图

1

题型：填空题

|

填空题 · 4 分

若将边长为的正方形绕其一条边所在直线旋转一周，则所形成圆柱的体积

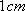
等于 .

正确答案

解析

略

知识点

由三视图还原实物图

1

题型：单选题

|

单选题 · 5 分

9．已知某几何体的三视图如图所示，根据图中标出的尺寸，可得这个几何体的表面积是

A4

B

C7＋

D5＋2＋

正确答案

D

解析

直观图如图所示

所以表面积为底面的面积加上4个侧面积，可得表面积为 5＋2＋，所以选D.

考查方向

空间几何体的三视图及表面积。

解题思路

先由三视图还原出直观图再求出其表面积。

易错点

不知道直观图是一个什么几何体。

知识点

由三视图还原实物图

1

题型：填空题

|

填空题 · 5 分

15.已知某空间几何体的三视图如图2所示，则该几何体的体积是．

正确答案

48

解析

将该几何体放到长方体中，由三视图可知原来的几何体为四棱锥，其中底面为直角梯形，上底长为2，下底长为6，高为6，四棱锥的高为6，所以其体积为。

考查方向

本题主要考查三视图和几何体的体积公式等知识，意在考查考生的空间想象能力和逻辑推理能力。

解题思路

将该几何体放到长发体中还原；利用棱锥的体积公式求解即可。

易错点

无法根据三视图将几何体还原；求几何体的体积时忘记乘以。

知识点

由三视图还原实物图

1

题型：单选题

|

单选题 · 5 分

6．某三棱锥的三视图如图2所示，则该三棱锥的体积是

A

B

C

D

正确答案

B

解析

如图所示，直观图是一个三棱锥，则其体积为，所以选B答案。

考查方向

空间几何体的三视图及其体积的计算。

解题思路

还原出直观图是一个三棱锥，然后按照体积的公式代入计算即可。

易错点

不会还原直观图。

知识点

由三视图还原实物图

1

题型：单选题

|

单选题 · 5 分

11．某工件的三视图如图所示，现将该工件通过切削，加工成一个体积尽可能大的长方体新工件，并使新工件的一个面落在原工件的一个面内，则原工件材料的利用率（材料利用率=新工件体积/原工件体积）为（）

A

B

C

D

正确答案

A

解析

由题设知：设长方体的高为，底面边长分别为，作圆锥的截面再结合由相似三角形可得：；所以，进而得：，当且仅当，即时取“=”号，故原工件材料的利用率为。所以答案应选A。

考查方向

本题主要考查了由三视图还原成实物图再进行体积的计算和求解内接长方体的体积。在近几年的各省高考题出现的频率较高，常是独立命题，求体积、表面积与棱长，也与函数结合求最值问题。

解题思路

由三视图先还原出实物的直观图，再计算出内接长方体的最大体积。

易错点

1、无法由三视图还原出实物直观图。2、圆锥内接长方体不会处理。

知识点

由三视图还原实物图

1

题型：填空题

|

填空题 · 5 分

16.已知△ABC中，角A、B、C成等差数列，且△ABC的面积为

，则AC边的最小值．

正确答案

2

解析

∵A、B、C成等差数列，∴，又，∴，

由得，∵，

及，∴，，∴b的最小值为2.

考查方向

本题主要考查等差中项、三角形的面积公式、余弦定理和基本不等式等知识，意在考查考生综合知识解决问题的能力。

解题思路

先根据角A、B、C成等差数列求出；利用三角形的面积公式求出，然后利用余弦定理表示出b后利用基本不等式求出最值。

易错点

不会将角A、B、C成等差数列转化得到角B的大小；求三角形的面积时不会利用基本不等式求最值。

知识点

等差数列的判断与证明由三视图还原实物图

热门试卷

正确答案

知识点

正确答案

知识点

正确答案

知识点

正确答案

解析

考查方向

解题思路

易错点

知识点

正确答案

解析

考查方向

解题思路

易错点

知识点

正确答案

解析

考查方向

解题思路

易错点

知识点

正确答案

解析

考查方向

解题思路

易错点

知识点

正确答案

解析

知识点

正确答案

解析

考查方向

解题思路

易错点

知识点

正确答案

解析

知识点

正确答案

解析

考查方向

解题思路

易错点

知识点

正确答案

解析

考查方向

解题思路

易错点

知识点

正确答案

解析

考查方向

解题思路

易错点

知识点

正确答案

解析

考查方向

解题思路

易错点

知识点

正确答案

解析

考查方向

解题思路

易错点

知识点