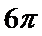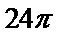- 立体几何与空间向量
- 共2637题
9. 某几何体的三视图如图所示，则该几何体外接球的表面积为 ( )
A
B
C
D
正确答案
解析
画出直观图，如图所示，几何体的外接球即为对应的棱长为1，1，2的长方体的外接球，所以2R=
考查方向
解题思路
借助长方体作出几何体的三视图如图所示，几何体的外接球，就是正方体的外接球，可直接算出球的表面积。
易错点
容易将几何体的三视图画错。
知识点
9．一个空间几何体的三视图如图所示，则这个几何体的表面积为
A
B
C
D
正确答案
解析
由三视图得，几何体为棱长都为
因为三棱锥的四个面全等，所以三棱锥的表面积
A选项不正确，C选项不正确，D选项不正确，所以选B选项。
考查方向
解题思路
由三视图得几何体为多面体；多面体的表面积为各个面面积之和。
易错点
由三视图推导不出原几何体的形状。
知识点
10. 已知一个几何体的三图如图所示，则该几何体的体积为( )
A
B
C
D
正确答案
解析
根据几何体的三视图，可知，立体图形是以高为2，底面积为2的两个集合组合体，根据几何体的体积公式利用底面积乘以高求得，所以选D
考查方向
简单空间图形的三视图
解题思路
本题考查由三视图还原几何体并且看出几何体各个部分的长度，
易错点
空间感不强，还原几何图形时 还原错误
教师点评
本题解题的关键是要求体积需要求出几何体的底面面积和高，三棱锥的高是由垂直与底面的侧面的高得到，本题是一个基础题．
知识点
9. 某几何体的三视图如图所示，则该几何体外接球的表面积为 ( )
A
B
C
D
正确答案
解析
画出直观图，如图所示，几何体的外接球即为对应的棱长为1，1，2的长方体的外接球，所以2R=
考查方向
解题思路
借助长方体作出几何体的三视图如图所示，几何体的外接球，就是正方体的外接球，可直接算出球的表面积。
易错点
容易将几何体的三视图画错。
知识点
6.已知某四棱锥的三视图如图所示，则该四棱锥的侧面积是
A
B
C
D
正确答案
解析
由三视图得四棱锥如下图所示，
故选B。
考查方向
解题思路
由三视图得到几何体为一个四棱锥。根据直观图计算各个侧面面积，即可。
易错点
本题在把几何体的还原成平面直观图上易出错。
知识点
请你谈一谈对“不同生产方式以及生产工艺中，生产物流管理所采用的方法和手段是不同的。”这句话的理解。
正确答案
测试
《算数书》竹简于上世纪八十年代在湖北省江陵县张家山出土，这是我国现存最早的有系统的数学典籍，其中记载有求“囷盖”的术：置如其周，令相乘也，又以高乘之，三十六成一，该术相当于给出了由圆锥的底面周长L与高h，计算其体积V的近似公式V≈
A
B
C
D
正确答案
解析
设圆锥底面圆的半径为r，高为h，则L=（2πr）2，
∴
∴π=
知识点
如图，网格纸上正方形小格的边长为1（表示1cm），图中粗线画出的是某零件的三视图，该零件由一个底面半径为3cm，高为6cm的圆柱体毛坯切削得到，则切削掉部分的体积与原来毛坯体积的比值为（ ）
A
B
C
D
正确答案
解析
几何体是由两个圆柱组成，一个是底面半径为3高为2，一个是底面半径为2，高为4，
组合体体积是：32π•2+22π•4=34π，底面半径为3cm，高为6cm的圆柱体毛坯的体积为：32π×6=54π。
切削掉部分的体积与原来毛坯体积的比值为：
知识点
如图，四棱锥P﹣ABCD中，底面ABCD为矩形，PA⊥平面ABCD，E为PD的中点。
（1）证明：PB∥平面AEC；
（2）设AP=1，AD=
正确答案
见解析。
解析
（1）证明：设BD与AC 的交点为O，连结EO，∵ABCD是矩形，∴O为BD的中点
∵E为PD的中点，∴EO∥PB，EO⊂平面AEC，PB⊄平面AEC∴PB∥平面AEC；
（2）∵AP=1，AD=
∴AB=
又
知识点
某三棱锥的侧视图、俯视图如图所示，则该三棱锥的体积是（锥体体积公式：
A3
B2
C
D1
正确答案
解析
由俯视图知该三棱锥的底面积
所以
知识点
如图，直三棱柱ABC－A′B′C′，∠BAC＝90°，AB＝AC＝λAA′，点M，N分别为A′B和B′C′的中点。
(1)证明：MN∥平面A′ACC′；
(2)求三棱锥A′－MNC的体积。
(锥体体积公式V＝
正确答案
见解析
解析
(1)证法一：连结AB′，AC′，由已知∠BAC＝90°，AB＝AC，三棱柱ABC－A′B′C′为直三棱柱，
所以M为AB′中点。
又因为N为B′C′的中点，
所以MN∥AC′。
又MN
因此MN∥平面A′ACC′。
证法二：取A′B′中点P，连结MP，NP，
而M，N分别为AB′与B′C′的中点，
所以MP∥AA′，PN∥A′C′，
所以MP∥平面A′ACC′，
PN∥平面A′ACC′。
又MP∩NP＝P，
因此平面MPN∥平面A′ACC′。
而MN
因此MN∥平面A′ACC′。
(2) (2)解法一：连结BN，由题意A′N⊥B′C′，平面A′B′C′∩平面B′BCC′＝B′C′，所以A′N⊥平面NBC。
又A′N＝
故VA′－MNC＝VN－A′MC＝
解法二：VA′－MNC＝VA′－NBC－VM－NBC＝
知识点
设图１是某几何体的三视图，则该几何体的体积为
A
B
C
D
正确答案
解析
有三视图可知该几何体是一个长方体和球构成的组合体，其体积
知识点
如图，正方体
正确答案
解析
以△
知识点
如图，四棱锥
（1）证明：
（2）若
正确答案
见解析
解析
（1）证明：连接
又
而
(2) 由（1）
知识点
一个几何体的三视图如图所示，则该几何体的体积为__________。
正确答案
12＋π
解析
如图所示，由已知得该几何体为一组合体，上面是底面圆半径为1，高为1的圆柱，下面是长为4，宽为3，高为1的长方体，如图所示。
故所求体积V＝π×12×1＋4×3×1＝12＋π。
知识点
扫码查看完整答案与解析