- 立体几何与空间向量
- 共2637题
19.如图，
（1）求证：
（2）求四棱锥
正确答案
（1）见解析；（2）
解析
试题分析：本题属于立体几何中的证明和求表面积问题，
（1）线线垂直转化为由线面垂直来证明；
（2）将每个面的面积算出来，最后相加即可。
（1）取
因为
所以
因此，
（2）设四棱锥
由于
所以
所以
综上，
考查方向
解题思路
本题考查立体几何的问题，解题步骤如下：（1）线线垂直转化为由线面垂直来证明；（2）将每个面的面积算出来，最后相加即可。
易错点
不会将线线垂直转化为由线面垂直来证明。
知识点
9．一个棱锥的三视图如图，则该棱锥的全面积是（ ）
A
B
C
D
正确答案
解析
解析已在路上飞奔，马上就到！
知识点
8．一个正四棱柱的各个顶点在一个直径为
正确答案
解析
解析已在路上飞奔，马上就到！
知识点
10. 若一个球的体积是
正确答案
128
解析
由题可知，球的半径为4，则正方体的棱长为a,3a2=64,所以表面积为128.
考查方向
解题思路
表示球内接正方体的棱长，即可得到结果。
易错点
本题易在求棱长时发生错误。
知识点
某几何体的三视图（如图3所示）均为边长为2的等腰直角三角
形，则该几何体的表面积是
A
B
C
D
正确答案
解析
略
知识点
一个空间几何体的三视图如图所示，该几何体的表面积为______.
正确答案
152
解析
略
知识点
若一个底面是正三角形的三棱柱的正视图如图2所示，则其表面积等于______.
正确答案
解析
略
知识点
若一个正方体的表面积为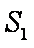
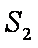
正确答案
解析
设正方体棱长为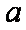
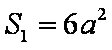
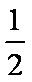
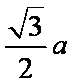
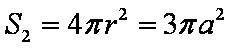
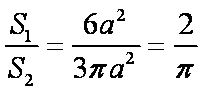
知识点
已知三棱锥
A表面积
B表面积为
C体积为
D体积为
正确答案
解析
略
知识点
10. 一个棱锥的三视图如图，则该棱锥的全面积为（ ）
A36+12
B48+24
C
D36+24
正确答案
解析
解析已在路上飞奔，马上就到！
知识点
16．已知三棱柱
正确答案
解析
因为侧棱垂直于底面，棱柱的体积为
考查方向
解题思路
利用垂直和棱柱体积求出AA1，再求出三角形ABC外接圆的半径，即可得到球的半径，从而求出球的表面积
易错点
计算能力；立体感
知识点
9．现有橡皮泥制作的底面半径为5，高为4的圆锥和底面半径为2，高为8的圆柱各一个，若将它们重新制作成总体积与高均保持不变，但底面半径相同的新的圆锥和圆柱各一个，则新的底面半径为 ．
正确答案
解析
由题意可知，原来圆锥和圆柱的体积和为：
设新圆锥和圆柱的底面半径为r，
则新圆锥和圆柱的体积和为：
∴
故答案为：
考查方向
解题思路
由题意求出原来圆柱和圆锥的体积，设出新的圆柱和圆锥的底面半径r，求出体积，由前后体积相等列式求得r．
易错点
本题考查了圆柱与圆锥的体积公式在计算半径时易错
知识点
《算数书》竹简于上世纪八十年代在湖北省江陵县张家山出土，这是我国现存最早的有系统的数学典籍，其中记载有求“囷盖”的术：置如其周，令相乘也，又以高乘之，三十六成一，该术相当于给出了由圆锥的底面周长L与高h，计算其体积V的近似公式V≈
A
B
C
D
正确答案
解析
设圆锥底面圆的半径为r，高为h，则L=（2πr）2，
∴
∴π=
知识点
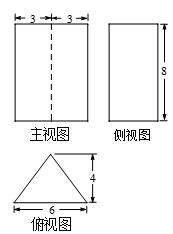
某三棱锥的侧视图、俯视图如图所示，则该三棱锥的体积是（锥体体积公式：
A3
B2
C
D1
正确答案
解析
由俯视图知该三棱锥的底面积
所以
知识点
18. 如图四边形ABCD为菱形，G为AC与BD交点，
（1）证明：平面
（2）若
正确答案
（1）因为四边形ABCD为菱形，所以AC⊥BD.
因为BE⊥平面ABCD,所以AC⊥BE,故AC⊥平面BED.
又AC
（2）设AB=
AG=GC=
因为AE⊥EC,所以在Rt△AEC中，可的EG=
由BE⊥平面ABCD,知△EBG为直角三角形，可得BE=
由已知得，三棱锥E-ACD的体积
故
从而可得AE=EC=ED=
所以△EAC的面积为3，△EAD的面积与 △ECD的面积均为
故三棱锥E-ACD的侧面积为3+2
解析
解析已在路上飞奔，马上就到！
知识点
扫码查看完整答案与解析