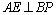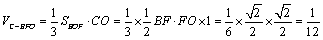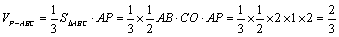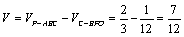- 立体几何与空间向量
- 共2637题
请你谈一谈对“不同生产方式以及生产工艺中,生产物流管理所采用的方法和手段是不同的。”这句话的理解。
正确答案
测试
如图,直三棱柱ABC-A′B′C′,∠BAC=90°,AB=AC=λAA′,点M,N分别为A′B和B′C′的中点。
(1)证明:MN∥平面A′ACC′;
(2)求三棱锥A′-MNC的体积。
(锥体体积公式V=
正确答案
见解析
解析
(1)证法一:连结AB′,AC′,由已知∠BAC=90°,AB=AC,三棱柱ABC-A′B′C′为直三棱柱,
所以M为AB′中点。
又因为N为B′C′的中点,
所以MN∥AC′。
又MN

因此MN∥平面A′ACC′。
证法二:取A′B′中点P,连结MP,NP,
而M,N分别为AB′与B′C′的中点,
所以MP∥AA′,PN∥A′C′,
所以MP∥平面A′ACC′,
PN∥平面A′ACC′。
又MP∩NP=P,
因此平面MPN∥平面A′ACC′。
而MN
因此MN∥平面A′ACC′。
(2) (2)解法一:连结BN,由题意A′N⊥B′C′,平面A′B′C′∩平面B′BCC′=B′C′,所以A′N⊥平面NBC。
又A′N=
故VA′-MNC=VN-A′MC=


解法二:VA′-MNC=VA′-NBC-VM-NBC=
知识点
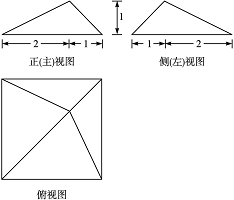
设图1是某几何体的三视图,则该几何体的体积为
正确答案
解析
有三视图可知该几何体是一个长方体和球构成的组合体,其体积
知识点
若某几何体的三视图(单位:cm)如图所示,则此几何体的体积是
正确答案
解析
选B,本题主要考察了对三视图所表达示的空间几何体的识别以及几何体体积的计算,属容易题
知识点
如图,四棱锥P﹣ABCD中,底面ABCD为矩形,PA⊥平面ABCD,E为PD的中点。
(1)证明:PB∥平面AEC;
(2)设AP=1,AD=

正确答案
见解析。
解析
(1)证明:设BD与AC 的交点为O,连结EO,∵ABCD是矩形,∴O为BD的中点
∵E为PD的中点,∴EO∥PB,EO⊂平面AEC,PB⊄平面AEC∴PB∥平面AEC;
(2)∵AP=1,AD=



∴AB=
又
知识点
如图,正方体


正确答案
解析
以△

知识点
如图,四棱锥



(1)证明:
(2)若


正确答案
见解析
解析
(1)证明:连接


又
而



(2) 由(1)

知识点
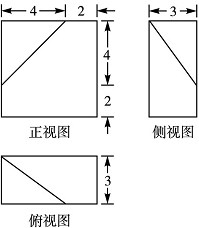
一个几何体的三视图如图所示,则该几何体的体积为__________。
正确答案
12+π
解析
如图所示,由已知得该几何体为一组合体,上面是底面圆半径为1,高为1的圆柱,下面是长为4,宽为3,高为1的长方体,如图所示。
故所求体积V=π×12×1+4×3×1=12+π。
知识点
某几何体的三视图(单位:cm)如图所示,则该几何体的的体积是( )
正确答案
解析
由三视图知,原几何体是由一个长方体与一个三棱柱组成,其体积为

知识点
某四棱锥的三视图如图所示,该四棱锥的体积为__________。
正确答案
3
解析
由三视图知该四棱锥底面为正方形,其边长为3,四棱锥的高为1,根据体积公式V=
知识点
已知某几何体的三视图(单位:cm)如图所示,则该几何体的体积是( )。
正确答案
解析
由三视图可知,该几何体是如图所示长方体去掉一个三棱锥,故几何体的体积是6×3×6-

知识点
某几何体的三视图如图所示,则该几何体的体积为( )
正确答案
解析
略
知识点
如图,几何体








(1)求异面直线

(2)求几何体
正确答案
见解析
解析
(1)解法一:在



由题意得,



∴




∵ 

∴
∴
则

所成的角.
由平面几何知识及勾股定理可以得
在

∵ 异面直线的夹角范围为
∴ 异面直线


解法二:
同解法一得


分别为
可得
∴ 
得
设向量


∵ 异面直线的夹角范围为
∴ 异面直线


(2)
如图,连结





∵

∴ 几何体
知识点
在直角梯形ABCD中,ADBC,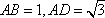
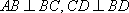
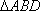
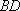
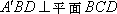
(1)求证: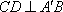
(2)求三棱锥
(3)在线段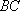
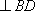
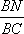
正确答案
见解析。
解析
(1)∵平面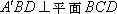
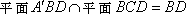
∴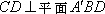
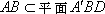
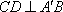
(2)如图(1)在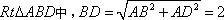
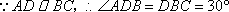
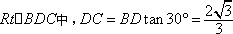
∴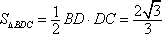
如图(2),在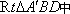
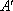

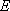
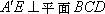
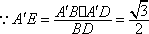
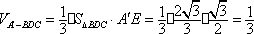
(3)在线段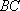
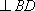
如图(2)在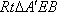
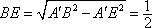
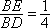
过点E做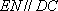
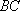
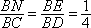
∵
又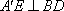
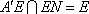
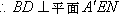
又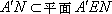
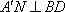
∴在线段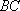
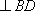
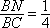
知识点
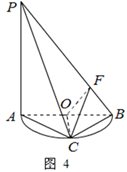
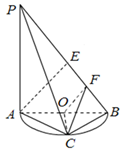
图4,PA垂直于⊙O所在平面ABC,AB为⊙O的直径,PA=AB=2,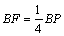
(1)证明:BC平面PAC;
(2)证明:CFBP;
(3)求四棱锥C—AOFP的体积.
正确答案
见解析。
解析
(1)
证明:∵PA⊥平面ABC,BC⊥平面ABC,
∴BC⊥PA.
∵△ACB是直径所对的圆周角,
∴
又∵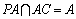
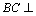
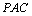
(2)证明:∵PA⊥平面ABC,OC⊥平面ABC,
∴OC⊥PA.
∵C是弧AB的中点,
∴△ABC是等腰三角形,AC=BC,
又O是AB的中点,∴OC⊥AB.
又∵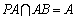
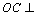
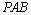
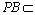
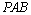
∴
设BP的中点为E,连结AE,则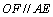
∴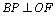
∵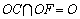
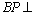
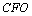
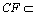
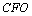
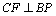
(3)解:由(2)知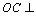
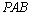
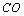

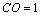
又∵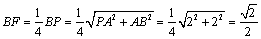
∴
又∵
∴四棱锥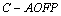
知识点
扫码查看完整答案与解析