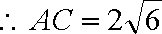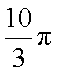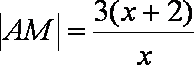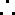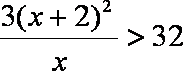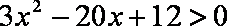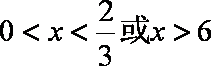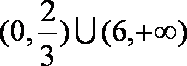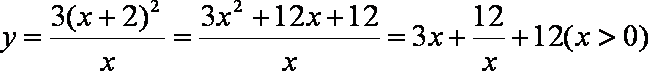- 立体几何与空间向量
- 共2637题
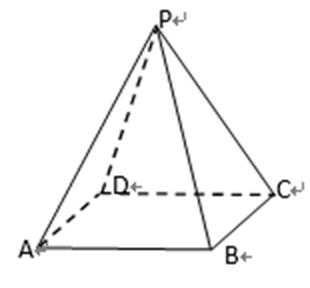
已知在正四棱锥

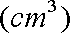


正确答案
见解析
解析
设异面直线


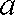
则依题意得 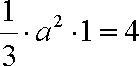
故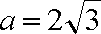
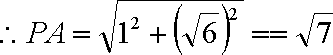



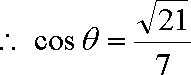
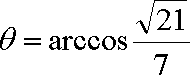
知识点
在长方体






(1)求棱
(2)求此几何体的表面积,并画出此几何体的主视图和俯视图(写出各顶点字母).
正确答案
见解析
解析
(1)设



(2)

主视图与俯视图各得2分
知识点
对于

若

正确答案
见解析
解析


知识点
在长方体





(1)求棱
(2)若



正确答案
见解析
解析
(1)设

(2)

在



知识点
在边长为4cm的正方形ABCD中,E、F分别为BC、CD的中点,M、N分别为AB、CF的中点,现沿AE、AF、EF折叠,使B、C、D三点重合,构成一个三棱锥.
(1)判别MN与平面AEF的位置关系,并给出证明;
(2)证明AB⊥平面BEF;
(3)求多面体E-AFNM的体积.
正确答案
见解析。
解析
(1)解析:
证明如下:
因翻折后B、C、D重合(如图),
所以MN应是
则
(2)因为

(3)方法一

∴
又
∴
方法二:

由(2)知AB即是三棱锥A-BEF的高,AB=4
MB即是三棱锥M-BEN的高,MB=2,


知识点
已知变量


正确答案
解析
根据题意作出不等式组所表示的可行域如图阴影部分所示,即








知识点
如图,矩形
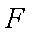
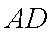
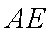
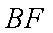

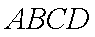
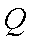
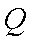
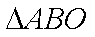
正确答案
解析
设矩形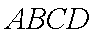
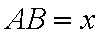
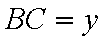
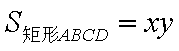


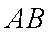
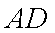
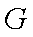
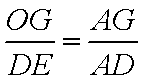
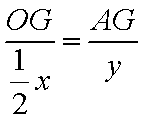
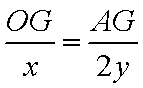
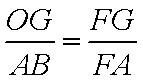
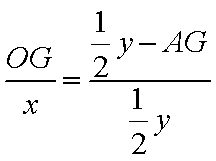
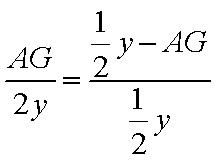
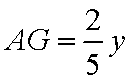
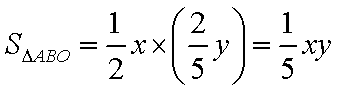
由几何概型的概率公式,得所求的概率为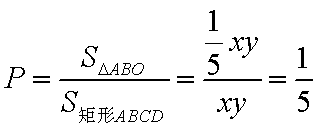
知识点
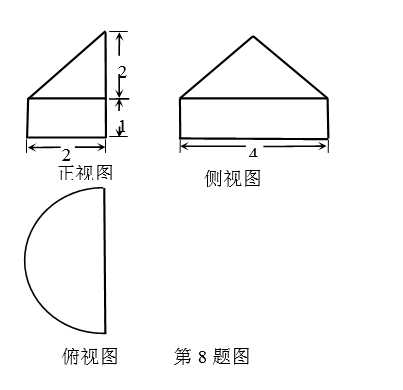
某几何体的三视图如图所示,则此几何体的体积是
正确答案
解析
此几何体为半个圆锥与半个圆柱的组合体,体积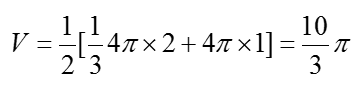
知识点
已知
(1)求
(2)将函数







正确答案
见解析
解析
(1)

所以

又由
得
故

(2)由















知识点
如图为某几何体的三视图,其中正视图是腰长为2的等腰三角形,侧视图是半径为1的半圆,则该几何体的表面积是_______________.
正确答案
解析
由三视图知,该几何体由两个共底面的半圆锥构成(如图所示),两个半圆锥侧面积的和为



知识点
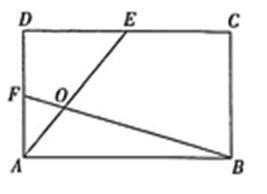
如图所示,将一矩形花坛ABCD扩建成一个更大的矩形花坛AMPN,要求B点在AM上,D点在AN上,且对角线MN过点C,已知AB=3米,AD=2米。
(1)要使矩形AMPN的面积大于32平方米,则DN的长应在什么范围内?
(2)当DN 的长度为多少时,矩形花坛AMPN的面积最小?并求出最小值。
正确答案
解析
(1)设DN的长为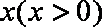
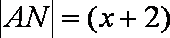
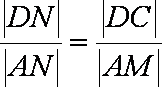
由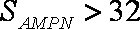
又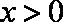
解得:
即DN的长取值范围是
(2)矩形花坛的面积为
当且仅当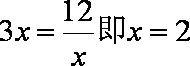
知识点
在直三棱柱ABC﹣A1B1C1中,AB⊥BC,D为棱CC1上任一点。
(1)求证:直线A1B1∥平面ABD;
(2)求证:平面ABD⊥平面BCC1B1。
正确答案
见解析
解析
证明:(1)由直三棱柱ABC﹣A1B1C1,得A1B1∥AB,
又EF⊄平面ABD,AB⊂平面ABD,
∴EF∥平面ABD。
(2)∵三棱柱ABC﹣A1B1C1为直三棱柱,∴AB⊥BB1,AB⊥BC,
∴AB⊥平面BCC1B1,
又∵AB⊂平面ABD,
∴平面ABD⊥平面BCC1B1。
知识点
已知向量


正确答案
见解析
解析


即


知识点
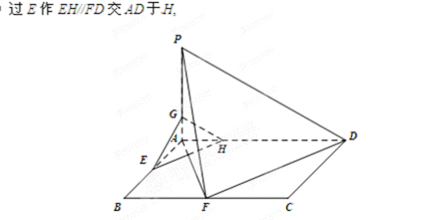
已知ABCD是矩形,AD=2AB,E,F分别是线段AB,BC的中点,PA⊥平面ABCD.
(1)求证:DF⊥平面PAF;
(2)在棱PA上找一点G,使EG∥平面PFD,当PA=AB=4时,求四面体E-GFD的体积.
正确答案
见解析
解析
(1)证明:在矩形ABCD中,因为AD=2AB,点F是BC的中点,
所以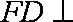
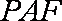
再过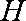
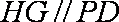
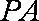
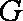
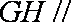
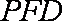
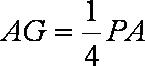
所以平面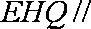
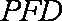
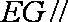
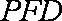
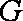
因为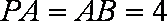
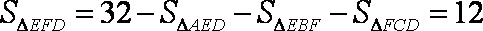
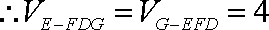
知识点
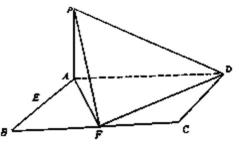
如图,在四棱锥


(1)求证:
(2)若


求证:平面

正确答案
见解析。
解析
(1)
取BD的中点O,连结EO,CO,∵△ABC为正三角形,且CD=CB
∴CO⊥BD,EO⊥BD
又

∴BD⊥EC.
(2)∵N是AB中点,
∵BC⊥AB,∴DN//BC,
∵BC

∵M为AE中点,N为AB中点,∴MN//BE,
∵MN

∵MN
知识点
扫码查看完整答案与解析