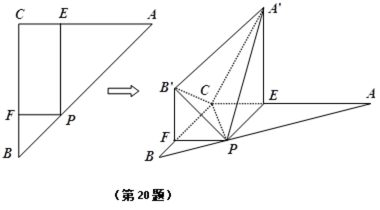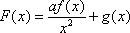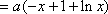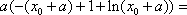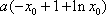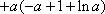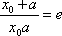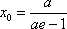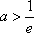- 立体几何与空间向量
- 共2637题
17.现需要设计一个仓库,它由上下两部分组成,上部的形状是正四棱锥

(1) 若AB=6 m,PO1=2 m,则仓库的容积是多少?
(2) 若正四棱锥的侧棱长为6 m,则当
正确答案
故仓库的容积为
(2)
当


当


因此,当

即
知识点
16. 如图,在四棱锥







(Ⅰ)

(Ⅱ)平面

(Ⅲ)求四棱锥
正确答案
(3)略
解析
解析已在路上飞奔,马上就到!
知识点
8.在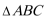
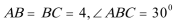
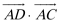
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
复数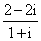
正确答案
-2i
解析
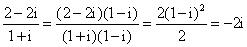
知识点
在空间,下列命题正确的是
正确答案
解析
由空间直线与平面的位置关系及线面垂直与平行的判定与性质定理可以很容易得出答案。
知识点
如图,EP交圆于E,C两点,PD切圆于D,G为CE上一点且PG=PD,连接DG并延长交圆于点A,作弦AB垂直EP,垂足为F。
(1)求证:AB为圆的直径;
(2)若AC=BD,求证:AB=ED。
正确答案
略。
解析
(1)∵PG=PD,∴∠PDG=∠PGD,
∵PD为切线,∴∠PDA=∠DBA,
∵∠PGD=∠EGA,
∴∠DBA=∠EGA,
∴∠DBA+∠BAD=∠EGA+∠BDA,
∴∠NDA=∠PFA,
∵AF⊥EP,
∴∠PFA=90°。
∴∠BDA=90°,
∴AB为圆的直径;
(2)连接BC,DC,则
∵AB为圆的直径,
∴∠BDA=∠ACB=90°,
在Rt△BDA与Rt△ACB中,AB=BA,AC=BD,
∴Rt△BDA≌Rt△ACB,
∴∠DAB=∠CBA,
∵∠DCB=∠DAB,
∴∠DCB=∠CBA,
∴DC∥AB,
∵AB⊥EP,
∴DC⊥EP,
∴∠DCE为直角,
∴ED为圆的直径,
∵AB为圆的直径,
∴AB=ED。
知识点
如图,在△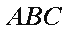

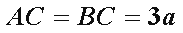
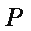
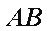
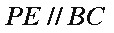
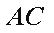
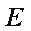
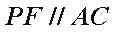
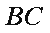

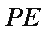
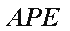
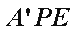
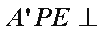
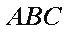
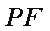
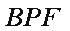
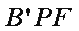
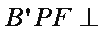
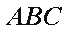
(1)求证: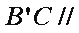

(2)若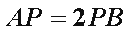
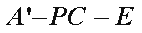
正确答案
见解析
解析
(1)因为
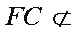
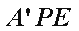

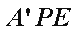
因为平面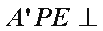
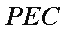
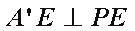
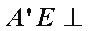
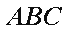
同理,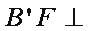
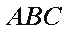
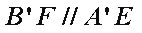
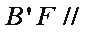
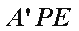
所以平面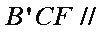
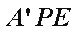
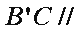
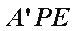
(2)因为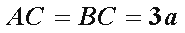
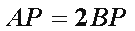
所以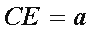

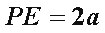
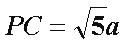
过E作
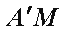
由(1)知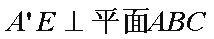

所以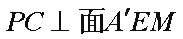

所以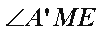
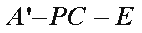
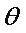
在Rt△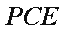
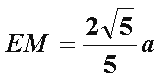
所以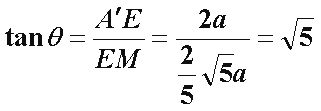
知识点
2008年3月31日,甲公司应收乙公司的一笔贷款500万元到期,由于乙公司发生财务困难,该笔贷款预计短期内无法收回。该公司已为该项债权计提坏账准备100万元。当日,甲公司就该债权与乙公司进行协商。下列协商方案中,属于甲公司债务重组的有 ( )。
A.减免100万元债务,其余部分立即以现金偿还
B.减免50万元债务,其余部分延期两年偿还
C.以公允价值为500万元的固定资产偿还
D.以现金100万元和公允价值为枷万元的无形资产偿还
E.以账面价值为600万元但公允价值为350万元的一批存货偿还
正确答案
A,B,E
解析
[解析] 债务重组是指在债务人发生财务困难的情况下,债权人按照其与债务人达成的协议或者法院的裁定作出让步的事项。选项CD债权人均没有作出让步,所以不属于债务重组。
底面边长为2m,高为1m的正三棱锥的全面积为 ▲ m2。
正确答案
解析
如图所示,正三棱锥









则



于是,

所以
知识点
如图,AB是半圆O直径,

正确答案
3
解析
试题分析:直角三角形ABC中,



知识点
已知函数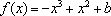
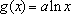
(1)若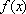
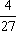
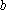
(2)若对任意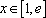
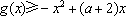

(3)若函数f(x)满足:在定义域内存在实数x0,使f(x0+k)= f(x0)+ f(k)(k为常数),则称“f(x)关于k可线性分解”. 设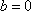
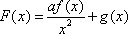

正确答案
见解析。
解析
(1)由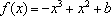
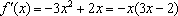
令
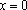

当
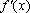
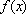
所以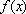
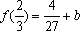
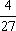
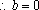
(2)由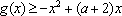
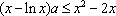
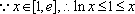
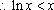
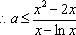
令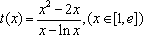
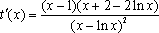
当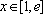
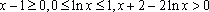
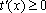
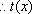
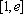
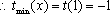
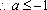
(3)证明:
由已知,存在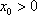
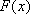
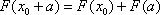
即:
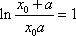
因为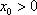
知识点
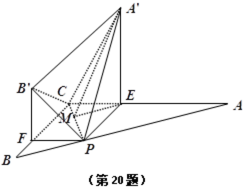
如图,四边形ABCD中,AB⊥AD,AD∥BC,AD=6,BC=4,AB=2,E、F分别在BC、AD上,EF∥AB,现将四边形ABEF沿EF折起,使得平面ABEF 
(1) 当



(2) 设BE=x,问当x为何值时,三棱锥A
正确答案
见解析。
解析
(1)存在

下面证明:
当









(2)因为平面ABEF







知识点
设a,b,c是空间三条直线,
正确答案
解析
略
知识点
已知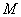
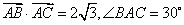
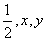
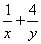
正确答案
解析
由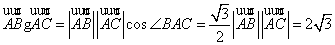
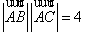
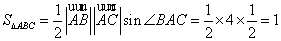
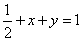
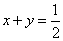
知识点
已知全集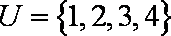
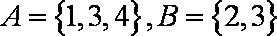
正确答案
解析
由韦恩图知: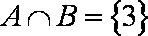
知识点
扫码查看完整答案与解析