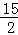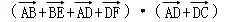- 立体几何与空间向量
- 共2637题
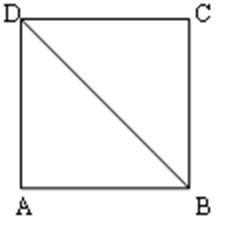
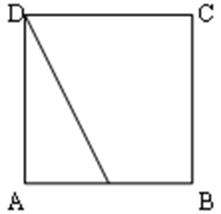
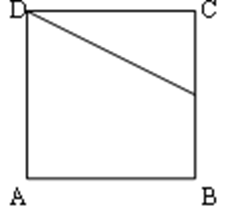
已知矩形ABCD中,AB=2,AD=1,E、F分别是BC、CD的中点,则(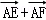
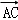
正确答案
解析
如图所示,
∵ 矩形ABCD中,E、F分别是BC、CD的中点,
∴ 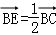
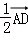
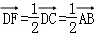
∴(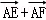
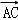
=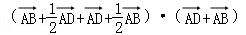
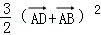
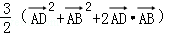
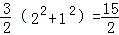
知识点
如图2,AB是⊙O的直径,BC是⊙O的切线,AC与⊙O交于点D,若
正确答案
4
解析
略
知识点
已知函数



(1)若




(2)求

(3)试探究能否存在区间







正确答案
见解析。
解析
(1)






(2)


令

若





若





若

由于



所以
综上可知
(3)






令
①若










②若




在









综上,当









知识点
设




① 若



③ 若


其中真命题的序号是
正确答案
解析
略
知识点
已知
正确答案
解析
略
知识点
一个四棱锥的三视图如图所示,其左视图是等边三角形,该四棱锥的体积= 。
正确答案
解析
略
知识点
对于平面α和直线m、n,下列命题是真命题的是
正确答案
解析
略
知识点
设

正确答案
解析
由图一、图二、图三分别可知选项A、B、C错误,根据线面垂直的性质可知选项D正确。
知识点
已知抛物线

正确答案
解析
略
知识点
已知



正确答案
解析
略
知识点
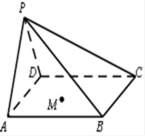
12.四棱锥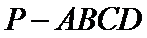
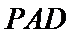
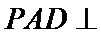
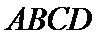
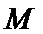
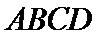

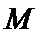
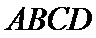
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
CD是正△ABC的边AB上的高,E,F分别是AC和BC边的中点,现将△ABC沿CD翻折成直二面角A-DC-B,如图所示.
(1)试判断折叠后直线AB与平面DEF的位置关系,并说明理由;
(2)若AC=2,求棱锥E-DFC的体积;
(3)在线段AC上是否存在一点P,使BP⊥DF?如果存在,求出
正确答案
见解析
解析
(1)AB∥平面DEF,理由如下:
如图:在△ABC中,由E、F分别是AC、BC中点,得EF∥AB,
(2)∵AD⊥CD,BD⊥CD,将△ABC沿CD翻折成直二面角A-DC-B。
∴AD⊥BD ∴AD⊥平面BCD
取CD的中点M,这时EM∥AD ∴EM⊥平面BCD,EM=1,

(3)在线段AC上存在点P,使AP⊥DE
证明如下:在线段AC上取点P,使AP=AC/3, 过P作PQ⊥CD于Q,
∴DF⊥平面BPQ, ∴BP⊥DF。
此时AP=

知识点
如图,EP交圆于E,C两点,PD切圆于D,G为CE上一点且PG=PD,连接DG并延长交圆于点A,作弦AB垂直EP,垂足为F。
(1)求证:AB为圆的直径;
(2)若AC=BD,求证:AB=ED。
正确答案
略。
解析
(1)∵PG=PD,∴∠PDG=∠PGD,
∵PD为切线,∴∠PDA=∠DBA,
∵∠PGD=∠EGA,
∴∠DBA=∠EGA,
∴∠DBA+∠BAD=∠EGA+∠BDA,
∴∠NDA=∠PFA,
∵AF⊥EP,
∴∠PFA=90°。
∴∠BDA=90°,
∴AB为圆的直径;
(2)连接BC,DC,则
∵AB为圆的直径,
∴∠BDA=∠ACB=90°,
在Rt△BDA与Rt△ACB中,AB=BA,AC=BD,
∴Rt△BDA≌Rt△ACB,
∴∠DAB=∠CBA,
∵∠DCB=∠DAB,
∴∠DCB=∠CBA,
∴DC∥AB,
∵AB⊥EP,
∴DC⊥EP,
∴∠DCE为直角,
∴ED为圆的直径,
∵AB为圆的直径,
∴AB=ED。
知识点
19.根据统计资料,某工艺品厂每日产品废品率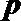
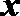
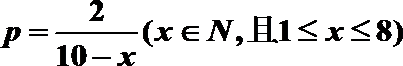
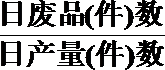
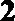
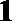
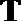
(1)将该车间日利润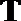
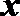
(2)当该车间的日产量为多少件时,日利润额最大?最大日利润额是几千元?
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
选做题(14、15题,只能从中选做一题)
14.(几何证明选讲选做题)










15.(坐标系与参数方程选做题)
极坐标方程分别是

正确答案
14.
15.
解析
解析已在路上飞奔,马上就到!
知识点
扫码查看完整答案与解析