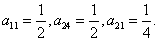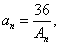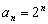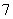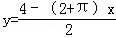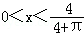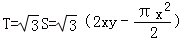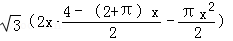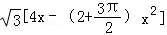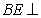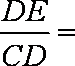- 立体几何与空间向量
- 共2637题
已知全集U=Z,集合A={0,1},B={-1,0,1,2},则图中阴影部分所表示的集合为
正确答案
解析
略
知识点
若函数

正确答案
解析
因为




据题意,
知识点
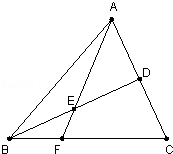
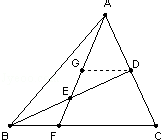
如图,在△ABC中,D是AC的中点,E是BD的中点,AE的延长线交BC于F。
(1)求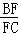
(2)若△BEF的面积为S1,四边形CDEF的面积为S2,求S1:S2的值。
正确答案
见解析。
解析
(1)过D点作DG∥BC,并交AF于G点,则易根据E是BD的中点,可得,△BEF≌△DEG,由全等三角形的性质可将BF:FC转化为DG:FC,再由平行线分线段成比例定理即可得到答案。
(2)△BEF以BF为底,△BDC以BC为底,由(I)的结论,我们可以求出两个三角形的底边长之比,及高之比,进而求出△BEF的面积S1,四边形CDEF的面积S2的比值。
解:(1)过D点作DG∥BC,并交AF于G点,∵E是BD的中点,∴BE=DE,
又∵∠EBF=∠EDG,∠BEF=∠DEG,∴△BEF≌△DEG,则BF=DG,∴BF:FC=DG:FC,
又∵D是AC的中点,则DG:FC=1:2,则BF:FC=1:2;即
(2)若△BEF以BF为底,△BDC以BC为底,则由(1)知BF:BC=1:3,
又由BE:BD=1:2可知h1:h2=1:2,其中h1、h2分别为△BEF和△BDC的高,
则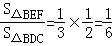
知识点
在





正确答案
4
解析
略
知识点
64个正数排成8行8列,如右图所示:
其中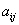
(1)求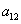

(2)记第n行各项之和为
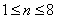
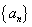
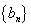
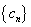
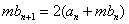
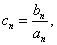
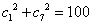
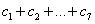
(3)对(2)中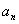
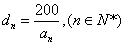
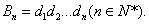

正确答案
见解析。
解析
(1)因为
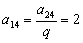
又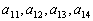
所以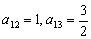
(2)由(1)得,第一行所成等差数列公差为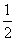
所以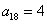
因为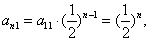
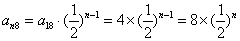
所以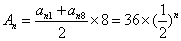
所以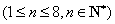
因为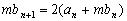
所以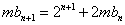
整理得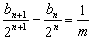
而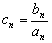
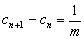
所以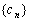
故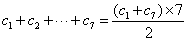
因为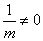
所以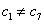
所以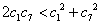
所以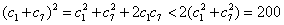
所以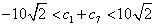
所以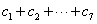
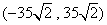
(3)因为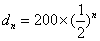
所以当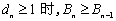
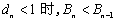
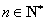
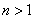
所以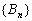
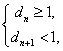
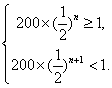
解得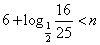
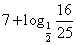
又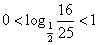
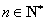
所以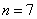
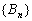
知识点
如图,在四棱锥






(1)求三棱锥
(2)求异面直线

正确答案
见解析
解析
(1)依题意,





∴
故
(2)∵




又∵





于是在



∴异面直线



知识点
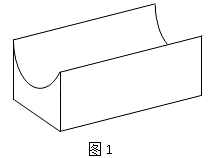
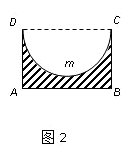
图1是某种称为“凹槽”的机械部件的示意图,图2是凹槽的横截面(阴影部分)示意图,其中四边形ABCD是矩形,弧CmD是半圆,凹槽的横截面的周长为4.已知凹槽的强度与横截面的面积成正比,比例系数为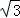
(1)写出y关于x函数表达式,并指出x的取值范围;
(2)求当x取何值时,凹槽的强度最大。
正确答案
见解析。
解析
(1)易知半圆CmD的半径为x,故半圆CmD的弧长为πx。
所以4=2x+2y+πx,
得
依题意知:0<x<y
得
所以,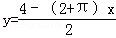
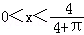
(2)依题意,设凹槽的强度为T,横截面的面积为S,则有
=
=
=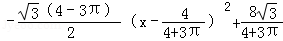
因为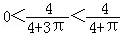
所以,当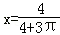
答:当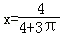
知识点
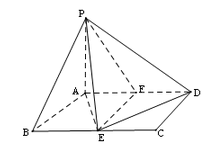
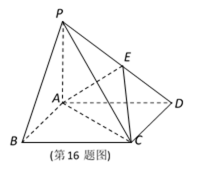
如图所示,四棱锥P-ABCD中,底面ABCD是边长为2的菱形,Q是棱
(1)若Q是PA的中点,求证:PC//平面BDQ;
(2)若PB=PD,求证:BD⊥CQ;
(3)在(2)的条件下,若PA=PC,PB=3,∠ABC=
正确答案
见解析
解析
(1)连结AC,交BD于O。
因为 底面ABCD为菱形,
所以 O为AC中点。
因为 Q是PA的中点,
所以 OQ// PC,
因为OQ

所以PC//平面BDQ。 ……………………5分
(2)因为 底面ABCD为菱形,
所以 AC⊥BD,O为BD中点。
因为 PB=PD,
所以 PO⊥BD。
因为 PO∩BD =O,
所以 BD ⊥平面PAC,因为 CQ
所以 B
(3)因为 PA=PC,
所以 △PAC为等腰三角形 。
因为 O为AC中点,
所以 PO⊥AC。
由(2)知 PO⊥BD,且AC∩BD =O,
所以 PO⊥平面ABCD,即PO为四棱锥P-ABCD的高。
因为四边形是边长为2的菱形,且∠ABC=60º,
所以BO=
所以PO=
所以 

知识点
矩形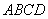
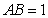

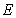
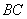
(1)求异面直线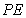
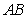
(2)求四棱锥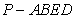
正确答案
(1)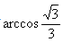
解析
解析:(1)取
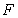
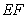
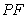
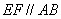
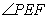
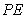
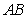
由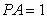
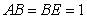
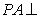
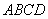
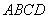
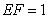
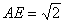
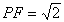
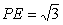
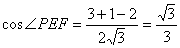

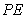
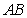
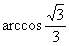
(2)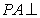
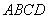
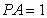
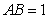
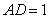
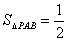
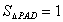
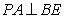
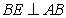
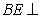
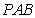
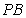
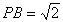
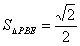
…………………………9分
连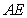
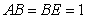
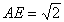
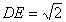
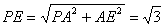
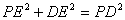
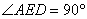
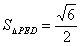

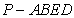
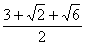
知识点
如图,在四棱锥P‐ABCD中,四边形ABCD为正方形,PA⊥平面ABCD,E为PD
的中点,求证:
(1)PB∥平面AEC;
(2)平面PCD⊥平面PAD。
正确答案
见解析
解析
(1)证明:连结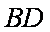
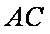

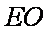
因为
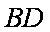
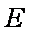
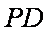
所以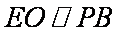
因为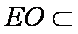
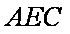
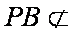
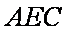
所以

(2)证明:因为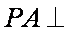
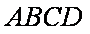
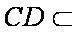
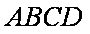
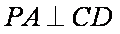
因为在正方形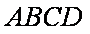
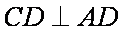
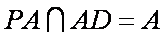
所以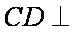

又因为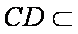
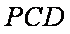
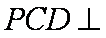

知识点
如图,在三棱柱



(1)求证:

(2)求证:直线

(3)设




正确答案
见解析
解析
(1)证明:因为三棱柱的侧面是正方形,
所以

所以

因为


由已知可得,底面
因为


因为


(2)证明:如图,连接



显然点

因为


又因为



所以直线

(3)在


此时点

过



由(1)可知



所以
又



又


知识点
设m、n是两条不同的直线,
正确答案
解析
举反例否定A、B、C
排除A、B、C
或直接据D推断
知识点
如图,在直三棱柱ABC-


(1)求证:
(2)当三棱锥


正确答案
见解析
解析
解析:(1)证明:连

又

另证:建立空间直角坐标系,证明
(2)设AE=
当且仅当
取





在
根据余弦定理得
知识点
如图,在底面为直角梯形的四棱锥P-ABCD中AD∥BC,∠ABC=90°PD⊥平面ABCD,AD=1,AB=
(1)求证:BD⊥PC;
(2)求直线AB与平面PDC所成的角;
(3)在线段PC上是否存在一点E,使得DE∥平面PAB?若存在,确定点E的位置;若不存在,请说明理由。
正确答案
见解析
解析
(1)证明:在直角△ABD中,AD=1,AB=
∴∠ABD=30°
∴∠DBC=60°
在△DBC中,CD2=BD2+BC2-2BD×BC×cos60°=4+16-2×2×4×
∴BC2=CD2+BD2,
∴BD⊥CD
∵PD⊥平面ABCD,BD⊂平面ABCD
∴PD⊥BD
∵PD∩CD=D
∴BD⊥平面PCD
∵PC⊂平面PCD
∴BD⊥PC;
(2)解:∵PD⊥平面ABCD,PD⊂平面ABCD。
∴平面PDC⊥平面ABCD。
过D作DF∥AB交BC于F,过点F作FG⊥CD交CD于G,则∠FDG为直线AB与平面PDC所成的角。
在Rt△DFC中,∠DFC=90°,DF=
∴tan∠FDG=
即直线AB与平面PDC所成角为60°。
(3)解:存在,且满足
连接EF,∵DF∥AB,∴DF∥平面PAB。
又∵DE∥平面PAB,DE∩DF=D
∴平面DEF∥平面PAB,
∵EF⊂平面DEF,∴EF∥AB。
又∵AD=1,BC=4,BF=1
∴
知识点
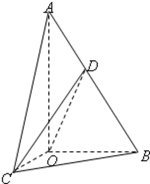
如图,在Rt△AOB中,∠OAB= 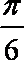
(1)求证:平面COD⊥平面AOB;
(2)求异面直线AO与CD所成角的大小。
(3)求CD与平面所AOB所成角的最大值.
正确答案
见解析
解析
(1)∵Rt△AOC可以通过Rt△AOB以直线AO为轴旋转得到
∴CO⊥AO,BO⊥AO
又∵二面角B-AO-C是直二面角
∴∠BOC是二面角B-AO-C的平面角
∴∠BOC=90°
∴CO⊥BO,又AO∩BO=O
∴CO⊥平面AOB
∵CO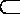
∴平面COD⊥平面AOB
(2)作DE⊥OB,垂足为E,连接CE,所以DE∥AO
∴∠CDE是异面直线AO与CD所成的角。
在 Rt△COE中,CO=BO=2,OE=
∴CE=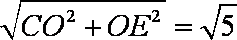

∴CD=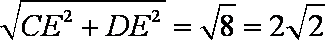
cos∠CDE=
∴异面直线AO与CD所成角为arcos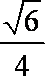
(3)由(I)知,CO⊥平面AOB(这是保证),∴∠CDO是CD与平面AOB所成的角,且tan∠CDO=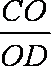
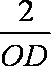
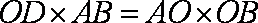
,tanCDO=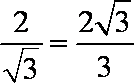
∴CD与平面AOB所成最大角的正切值为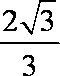
知识点
扫码查看完整答案与解析