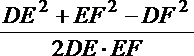- 立体几何与空间向量
- 共2637题
5.已知向量




正确答案
解析
解析已在路上飞奔,马上就到!
知识点
8.已知函数
①定义域为实数集R;
②

③当x∈[-1,1]时,
则方程
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
如图,三棱柱ABC-A1B1C1的侧棱AA1⊥底面ABC,∠ACB=90°,E是棱CC1的中点,F是AB的中点,AC=BC=1,AA1=2.
(1)求证:CF∥平面AB1E;
(2)求三棱锥C-AB1E在底面AB1E上的高。
正确答案
见解析
解析
(1)取AB1的中点G,连接EG,FG,
∵F、G分别是AB、AB1的中点,∴FG∥BB1,FG=BB1.
∵E为侧棱CC1的中点,∴FG∥EC,FG=EC,∴四边形FGEC是平行四边形,
∴CF∥EG,∵CF⊄平面AB1E,EG⊂平面AB1E,∴CF∥平面AB1E. …… 6分
(2)∵三棱柱ABC-A1B1C1的侧棱AA1⊥底面ABC,∴BB1⊥平面ABC.
又AC⊂平面ABC,∴AC⊥BB1,∵∠ACB=90°,∴AC⊥BC,
∵BB1∩BC=B,∴AC⊥平面EB1C,∴AC⊥CB1,
∴VA-EB1C=S△EB1C·AC=××1=。
∵AE=EB1=,AB1=,∴S△AB1E=,∵VC-AB1E=VA-EB1C,
∴三棱锥C-AB1E在底面AB1E上的高为=. …… 12分
知识点
函数
正确答案
解析
通过观察图像可知函数图像过






知识点
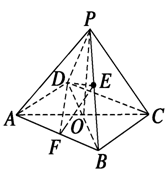
如图,平面四边形









(1) 证明:平面

(2)求点

正确答案
见解析。
解析
(1) 证明:

则




(2)由图可知
则



知识点
已知函数
(1) 当

(2)当



正确答案
(1)函数f(x)的单调递增区间为(-1,1),单调递减区间为(1,+∞)
(2)(-∞,0]
解析
(1) 当


由



故函数


(2)因函数

则当


设


由
(i) 当

当




(ii) 当



① 若



则函数





② 若




同样



(iii) 当



∴



综上所述,实数a的取值范围是
知识点
已知向量





(1) 求函数
(2) 在




求
正确答案
见解析。
解析
(1) 



(2)由(1)知
∴
又∵A是△ABC的内角,
∴
由余弦定理:
由正弦定理
知识点
如图,在四棱锥S-ABCD中,SA=AB=2,SB=SD=2
(1)证明:CD⊥平面SAE;
(2)侧棱SB上是否存在点F,使得CF∥平面SAE?并证明你的结论。
正确答案
见解析
解析
(1) 



又


则有



又


由




(2)



设


则
















知识点
已知双曲线


正确答案
解析
由题可知,双曲线渐近线的倾角为





知识点
11.一个几何体的三视图如图所示,则这个几何体的侧面积等于__________
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
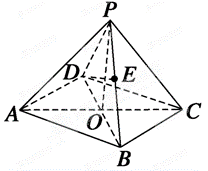
19.如图所示,在四棱锥P—ABCD中,底面是边长为2的菱形,∠DAB=60°,对角线AC与BD交于点O,PO⊥平面ABCD,PB与平面ABCD所成角为60°.
(1)求四棱锥的体积;
(2)若E是PB的中点,求异面直线DE与PA所成角的余弦值.
正确答案
(1)在四棱锥P—ABCD中,
∵PO⊥平面ABCD,
∴∠PBO是PB与平面ABCD所成的角,
即∠PBO=60°,
在R
∵BO=AB·sin30°=1,
又PO⊥OB,∴PO=BO·tan60°=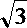
(2)
取AB的中点F,连接EF,DF,
∵E为PB中点,∴EF∥PA,
∴∠DEF为异面直线DE与PA所成角(或其补角).
在Rt△AOB中,
AO=AB·cos30°=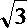
∴在Rt△POA中,PA=6,∴EF=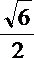
在正三角形ABD和正三角形PDB中,DF=DE=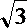
由余弦定理得
∴cos∠DEF=
=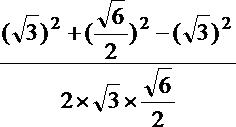
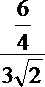
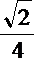
所以异面直线DE与PA所成角的余弦值为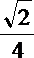
解析
解析已在路上飞奔,马上就到!
知识点
18.已知各项均为正数的等比数列




(1)求数列
(2)设







正确答案
解析
解析已在路上飞奔,马上就到!
知识点
9. 过抛物线





正确答案
解析
解析已在路上飞奔,马上就到!
知识点
16.定义在R上的函数

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
6.已知数列


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
扫码查看完整答案与解析