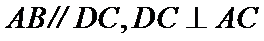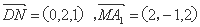- 立体几何与空间向量
- 共2637题
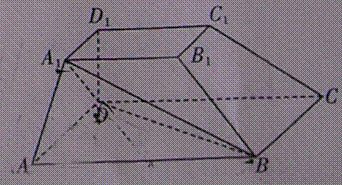
18.如图,在四棱锥P-ABCD中,PC⊥平面ABCD,
(I)求证: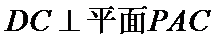
(II)求证: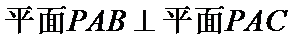
(III)设点E为AB的中点,在棱PB上是否存在点F,使得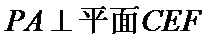
正确答案
知识点
选修4-1:几何证明选讲
如图,在正方形ABCD中,E,G分别在边DA,DC上(不与端点重合),且DE=DG,过D点作DF⊥CE,垂足为F.
(Ⅰ)证明:B,C,G,F四点共圆;
(Ⅱ)若AB=1,E为DA的中点,求四边形BCGF的面积.
23选修4-4:坐标系与参数方程
在直角坐标系xOy中,圆C的方程为
(Ⅰ)以坐标原点为极点,x轴的正半轴为极轴建立极坐标系,求C的极坐标方程;
(Ⅱ)直线l的参数方程是

24选修4-5:不等式选讲
已知函数

(Ⅰ)求M;
(Ⅱ)证明:当a,b

正确答案
22(I)因为
则有
所以
由此

(II)由



由



因此四边形



23(I)由

(II)在(I)中建立的极坐标系中,直线
由



于是
由

所以


24(I)
当



当

当



所以

(II)由(I)知,当


因此
知识点
10.一个三棱锥的正视图和俯视图
正确答案
解析
选项A,B的情况结合正视图和俯视图都构不成三棱锥,C选项中有虚线部分,D选项中没有,结合实际情况,三棱锥不可能出现C中的情况,所以选D
考查方向
解题思路
先根据正视图和俯视图想象出侧视图的大致情况,然后根据选项判断
易错点
三视图还原成立体图错误
知识点
1.
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
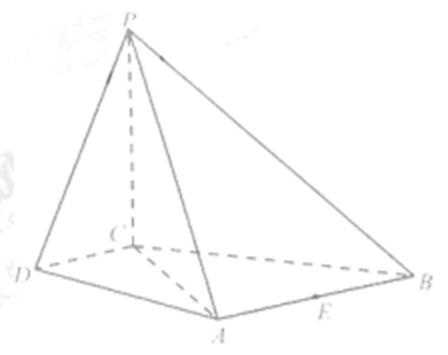
15.如图,在正四棱柱ABCD-A1B1C1D1中,E为CC1的中点,AB=1,CC1=
正确答案
解析
如图,连接AC,交BD于点O,连接OE, 
∴直线AC1到平面BDE的距离即为点A到平面BDE的距离,设为h.由等体积法,得


知识点
8.已知命题“



正确答案
解析
解析已在路上飞奔,马上就到!
知识点
请你谈一谈对“不同生产方式以及生产工艺中,生产物流管理所采用的方法和手段是不同的。”这句话的理解。
正确答案
测试
底面边长为2的正三棱锥



正确答案
解析
在△


故
同理,

设Q是△ABC的中心,则PQ⊥平面ABC,
所以
从而,
知识点
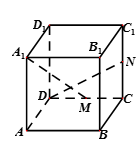
如图,在正方体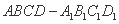
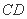
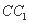
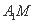
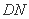
正确答案
90º
解析
方法一:连接D1M,易得DN⊥A1D1 ,DN⊥D1M,
所以,DN⊥平面A1MD1,
又A1M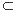
方法二:以D为原点,分别以DA, DC, DD1为x, y, z轴,建立空间直角坐标系D—xyz.设正方体边长为2,则D(0,0,0),N(0,2,1),M(0,1,0)A1(2,0,2)
故,
所以,cos<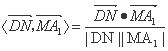
知识点
如图,在四棱台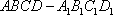
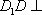
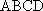
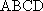
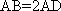
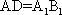
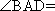
(1)证明: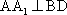
(2)证明: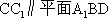
正确答案
见解析。
解析
(1)证明:因为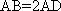
AD=a,则AB=2a,又因为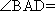
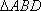
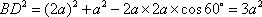
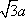

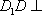
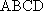


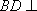
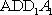
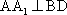
(2)连结AC,设AC
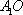
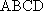
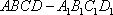
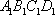
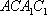
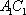
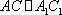
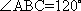
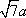
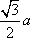
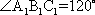
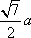


知识点
已知正方体

正确答案
解析
取A1B1的中点M连接EM,AM,AE,则


知识点
(

正确答案
解析
知识点
(1-3x)5的展开式中x3的系数为( )
正确答案
解析
(1-3x)5的展开式的通项为Tr+1=

知识点
设双曲线的左准线与两条渐近线交于

正确答案
解析
设双曲线为



以AB为直径的圆:



即

知识点
设函数
(1)求
(2)若函数


求

正确答案
(1) 
解析
(1)
故
(2)依题意
当
所以
知识点
扫码查看完整答案与解析