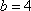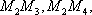- 立体几何与空间向量
- 共2637题
如图,几何体








(1)求异面直线

(2)求几何体
正确答案
见解析
解析
(1)解法一:在



由题意得,



∴




∵ 

∴
∴
则

所成的角.
由平面几何知识及勾股定理可以得
在

∵ 异面直线的夹角范围为
∴ 异面直线


解法二:
同解法一得


分别为
可得
∴ 
得
设向量


∵ 异面直线的夹角范围为
∴ 异面直线


(2)
如图,连结





∵

∴ 几何体
知识点
在长方体






(1)求异面直线
(2)求以
正确答案
(1)
解析
联结


又

∴

由

∴


(2)由题意可知,点


∴
∵
∴
知识点
把正方形ABCD沿对角线BD折成直二面角,对于下面结论:①AC⊥BD;②CD⊥平面ABC;③AB与BC成600角;④AB与平面BCD成450角。则其中正确的结论的序号为
正确答案
解析
略
知识点
如图,四棱锥



(1)求证:
(2)求异面直线

正确答案
见解析
解析
(1)∵

∴CD⊥SD
又四边形ABCD是正方形,∴CD⊥AD
∴CD⊥平面SDA

∴SA⊥CD.
(2)∵
∴


由(1),BA⊥平面SDA,∴△SAB是直角三角形.

故异面直线SB与CD所成角的大小为
知识点
如图,在直三棱柱









正确答案


解析
直三棱柱
所以


直三棱柱

由点

直三棱柱

所以

所以异面直线



知识点
已知函数






正确答案
-1
解析
略
知识点
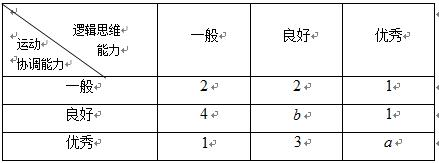
某单位从一所学校招收某类特殊人才,对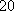
例如表中运动协调能力良好且逻辑思维能力一般的学生是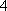
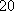

(1)求
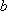
(2)从运动协调能力为优秀的学生中任意抽取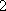
正确答案
(1)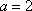
(2)
解析
(1)由题意可知,逻辑思维能力优秀的学生共有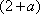
设事件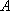
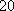
则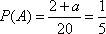
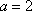
(2)由题意可知,运动协调能力为优秀的学生共有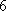
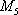
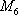
从中任意抽取
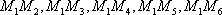
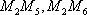
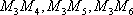
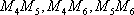
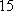
设事件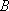
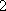
事件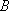
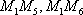
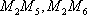
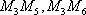
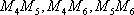
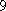
所以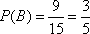
所以至少有一位逻辑思维能力优秀的学生的概率为
知识点
已知正方体

(1)求异面直线

(2)求四棱锥
正确答案
(1)
解析
(1)因为 





又




(2)四棱锥
知识点
如图,在直三棱柱






(1)求三棱锥
(2)求异面直线

正确答案
(1)
解析
(1)
(2)连接




在


所以异面直线


知识点
如图,正方形ADEF所在平面和等腰梯形所在平面ABCD垂直,已知BC=2AD=4,
(1)
(2)求异面直线BE与AF所成的角;
(3)求该几何体的表面积。
正确答案
见解析。
解析
知识点
如图所示的长方体








(1)求证:

(2)求三棱锥
正确答案
见解析。
解析
(1)
连结
∵




∴四边形
∴
∵



∴

(2)解法1 连结






∴
又∵在长方体



∴



∴

∴



∵
∴
解法2: 三棱锥










知识点
四棱锥P-ABCD的底面是边长为1的正方形,PD⊥底面ABCD,点E在棱PB上。
(1)求证:平面AEC⊥平面PDB
(2)当PD=且E为PB的中点时,求AE与平面PDB所成角的大小。
正确答案
见解析
解析
(1)证明:∵AC,BD是正方形ABCD的对角线
∴AC⊥BD
∵PD⊥底面ABCD,AC
∴PD⊥AC
∵PD∩BD=P
∴AC⊥面PDB
又∵AC
∴面ACE面PDB
(2)设AC与BD交于一点O,连接EO
由上题知:AC⊥面PDB
∴EO是斜线AE在平面PDB内的射影,AO⊥EO

在
∴
在边长为1的正方形ABCD中,AO=
∴
∴
知识点
如图,已知边长为8米的正方形钢板有一个角锈蚀, 其中






正确答案
48
解析
略
知识点
如图,四棱锥P—ABCD中,PA


(1)求证:MN//平面PDC;
(2)求三棱锥N—PAC的体积。
正确答案
见解析。
解析
知识点
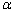
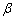
(1)a∥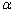
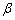
(2)a⊥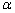
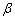
(3)a⊥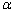
(4)a∥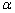
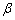
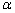
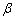
正确答案
解析
由题意知(3)满足条件,∴有一个。
知识点
扫码查看完整答案与解析