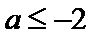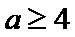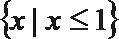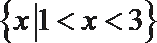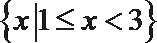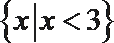- 立体几何与空间向量
- 共2637题
19.已知集合 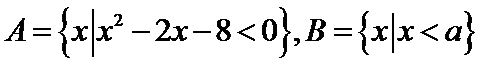
(1)若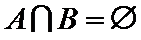
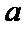
(2)若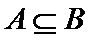
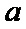
正确答案
(1)
(2)
解析
解析已在路上飞奔,马上就到!
知识点
5.空间四边形ABCD的两条对角线AC和BD的长分别为6和4,它们所成的角为900,则四边形两组对边中点的距离等于 ( )
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
14.在正三角形ABC中,D、E、F分别是AB、BC、AC的中点,G、H、M分别为DE、FC、EF的中点,将
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
23.已知以a为首项的数列
(1)若0<

(2)若a,k∈N﹡,求使
(3)若


正确答案
(1)当

当

故
所以当
总有
(2)①当


同理可得,当

当

②当

③当
综上得:当

当

(3)由m


当




解析
解析已在路上飞奔,马上就到!
知识点
11.在正方体


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
21.如图,在四棱锥









(1)证明:直线
(2)求异面直线

正确答案
方法一(综合法)
(1)取OB中点E,连接ME,NE
又
(2)



连接

所以 

方法二(向量法)作
如图,分别以AB,AP,AO所在直线为

(1)
设平面OCD的法向量为

即

(2)设





解析
解析已在路上飞奔,马上就到!
知识点
1.已知集合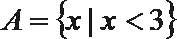
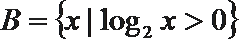

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
16.关于正四棱锥
①异面直线
②侧面为锐角三角形;
③侧面与底面所成的二面角大于侧棱与底面所成的角;
④相邻两侧面所成的二面角为钝角;
其中正确的命题序号是___________。
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
4.设函数f(x)=


正确答案
解析
由题意可得,f(x0)=±



再由

∴m2 >
∴m2>4,解得m>2或m<-2.
知识点
6.半圆的直径AB=4,O为圆心,C是半圆上不同于A、B的任意一点,若P为半径OC上的动点,则
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
11.平面



正确答案
知识点
19.如图,圆锥的顶点为










正确答案
解析
试题分析:因为

所以三棱锥

因为




在


过


在

所以异面直线


考查方向
解题思路
求异面直线所成的角常采用“平移线段法”,平移的方法一般有三种类型:利用图中已有的平行线平移;利用特殊点(线段的端点或中点)作平行线平移;补形平移.计算异面直线所成的角通常放在三角形中进行.
易错点
异面直线所成角的寻找
知识点
19.如图,圆锥的顶点为




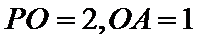
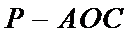


正确答案
三棱锥


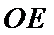
解析
解:

所以∠PAC为异面直线PA与OE所成的角或其补角.
由PO=2,OA=OC=1,得PA=PC=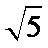
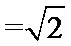
在△PAC中,由余弦定理得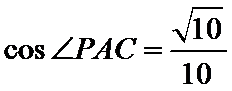
故异面直线PA与OE所成角的大小为
知识点
7.设α为平面,a、b为两条不同的直线,则下列叙述正确的是( )
正确答案
解析
对于A答案,直线a与b可以相交,也可以异面,也可以平行;
对于B答案,b和a垂直,但是和平面α的关系不能确定,也可以在平面α内;
对于D答案,b和a垂直,但是和平面α的关系不能确定,可以和平面α斜交。
所以,A选项不正确, C选项不正确,D选项不正确,B选项正确。
考查方向
解题思路
1.对每一个选项进行判断即可;
2.也可以画出图形,直接判断。
A选项不正确, C选项不正确,D选项不正确,B选项正确。
易错点
本题在线线平行、线面平行,线线垂直、线面垂直上容易混淆。有些关系没有考虑到导致出错。
知识点
19.如图,四棱柱








(Ⅰ)证明:平面

(Ⅱ)若


正确答案
见解析
解析
试题分析:本题属于立体几何中的基本问题,题目的难度是逐渐由易到难.
试题解析:(Ⅰ)依题意


∵








(Ⅱ)取






∴四边形
可得



即异面直线


考查方向
本题考查了立体几何中的面面垂直和异面直线所成的角的问题.属于高考中的高频考点。
解题思路
本题考查立体几何,解题步骤如下:
(1)转化为证明线面垂直。
(2)找到三角形,利用余弦定理求解。
易错点
(1)第一问中的面面垂直的转化。(2)第二问中异面直线所成的角求解时要找到适当的三角形。
知识点
扫码查看完整答案与解析