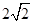- 立体几何与空间向量
- 共2637题
16.已知一个棱长为
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
6.正四面体







正确答案
1
解析
解析已在路上飞奔,马上就到!
知识点
请你谈一谈对“不同生产方式以及生产工艺中,生产物流管理所采用的方法和手段是不同的。”这句话的理解。
正确答案
测试
有一面8 m长的墙,用12 m长的篱笆和这面墙一起围成一个矩形场地(墙面的一部分或整个墙面作为矩形的一边),则它的最大面积是 ——m2.
正确答案
18
解析
略
知识点
如图,已知正四棱柱





(1)求异面直线

(2)求过

正确答案
(1)
解析
(1)连结




在


所以异面直线

(2)









知识点
如图,在直三棱柱









正确答案


解析
直三棱柱
所以


直三棱柱

由点

直三棱柱

所以

所以异面直线



知识点
下列结论:
①直线a,b为异面直线的充要条件是直线a,b不相交;
②从总体中抽取的样本(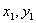
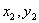
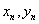
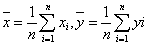

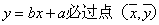
③函数
④已知函数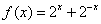
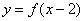
其中正确的结论是 .(注:把你认为正确结论的序号都填上)
正确答案
②④
解析
略
知识点
在复平面内,复数
正确答案
解析
略
知识点
矩形ABCD中,若
正确答案
(1,3)
解析
略
知识点
过点(2,1)作圆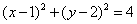
正确答案
解析
略
知识点
题(本大题共有5题,满分74分)解答下列各题必须在答题纸相应编号的规定区域内写出必要的步骤.
本题共有2个小题,第1小题满分6分,第2小题满分6分.
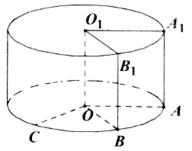
将边长为1的正方形AA1O1O(及其内部)绕OO1旋转一周形成圆柱,如图,
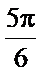
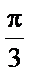
19.求圆柱的体积与侧面积;
20.求异面直线O1B1与OC所成的角的大小.
正确答案
圆柱的体积为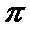
解析
由题意可知,圆柱的母线长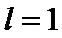
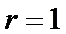
圆柱的体积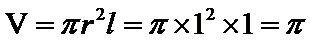
圆柱的侧面积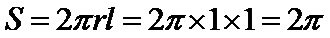
考查方向
解题思路
体积面积公式
易错点
用错公式
正确答案
异面直线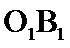
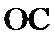
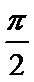
解析
设过点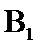
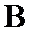
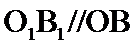
所以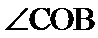
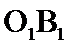
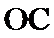
由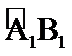
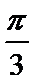
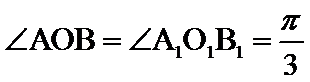
由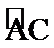
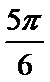
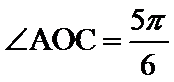
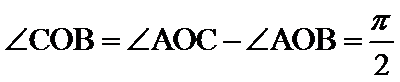
所以异面直线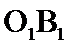
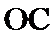
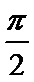
考查方向
解题思路
平移法解决异面直线夹角问题;
易错点
弧长公式
5.


正确答案
解析
根据充分条件和必要条件的定义结婚空间直线的位置关系,进行则l1,l2可能是平行或异面直线,即必要性不成立,
故p是q的充分条件,但不是q的必要条.
考查方向
解题思路



易错点
粗心选错。
知识点
5.设A1,A2,A3,A4是平面直角坐标系中两两不同的四个点,若


正确答案
解析
根据题意可知





知识点
在空间,下列命题正确的是
正确答案
解析
由空间直线与平面的位置关系及线面垂直与平行的判定与性质定理可以很容易得出答案。
知识点
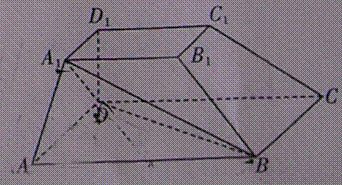
如图,在四棱台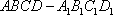
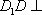
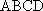
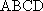
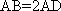
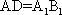
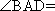
(1)证明: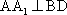
(2)证明: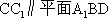
正确答案
见解析。
解析
(1)证明:因为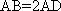
AD=a,则AB=2a,又因为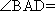
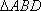
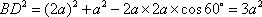
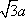

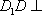
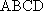


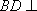
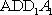
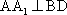
(2)连结AC,设AC
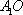
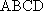
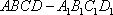
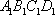
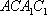
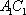
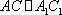
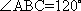
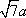
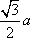
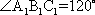
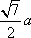
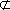


知识点
扫码查看完整答案与解析