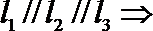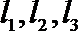- 立体几何与空间向量
- 共2637题
已知点







正确答案
解析
略
知识点
如图,在三棱柱ABC﹣A1B1C1中,侧棱AA1⊥底面ABC,AB⊥BC,D为AC的中点,AA1=AB=2。
(1)求证:AB1∥平面BC1D;
(2)若BC=3,求三棱锥D﹣BC1C的体积。
正确答案
见解析。
解析
(1)
证明:连接B1C,设B1C与BC1相交于O,连接OD,
∵四边形BCC1B1是平行四边形,∴点O为B1C的中点。
∵D为AC的中点,
∴OD为△AB1C的中位线,∴OD∥B1A。
OD⊂平BC1D,AB1⊄平面BC1D,
∴AB1∥平面BC1D。
(2)∵三棱柱ABC﹣A1B1C1,∴侧棱CC1∥AA1,
又∵AA1底面ABC,∴侧棱CC1⊥面ABC,
故CC1为三棱锥C1﹣BCD的高,A1A=CC1=2,
∴
∴
知识点
已知正方体的棱长为1,其俯视图是一个面积为1的正方形,侧视图是一个面积为
正确答案
解析
略。
知识点
如图,在正方体







正确答案
解析
略
知识点
在直三棱柱




(1)求证:
(2)若




正确答案
见解析。
解析
(1)
证明:



又






又 






又


(2)在直三棱柱







在



在
由(1)知





知识点
如图,弧
















(1)求异面直线

(2) 将

正确答案
(1)
解析
(1) 








(2)连结


由题设知,所得几何体为圆锥,其底面积为

该圆锥的体积为
知识点
已知









正确答案
解析
略
知识点
如图所示,在直三棱柱





(1)求证: 
(2)当面

(3)在(2)结论下,证明:

正确答案
见解析。
解析
证明:(1)设AB中点为G,连结GE,GC。

又EG∥
又
又因为MN//AB,所以
而
(2)因为面

面

面
所以
所以D为
(3)
因为EG//



所以


所以
又AB⊥CE,
所以

(3)方法二(略证):
过E点作

可用初中三角形相似或建立平面坐标系利用向量,直线斜率等方法证明
又
所以
所以
所以
又
所以
知识点
如图,四棱锥




(1)若



(2)若



正确答案
见解析
解析
证明:
(1)取

因为



所以

所以
因为



所以

(2)
取





∵


∴
∵


∴










∴




∵





∴

知识点
6.设

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
8.用a,b,c表示三条不同的直线,γ表示平面,给出下列命题:
①若a∥b,b∥c,则a∥c;
②若a⊥b,b⊥c,则a⊥c;
③若a∥γ,b∥γ,则a∥b;
④若a⊥γ,b⊥γ,则a∥b.
其中真命题的序号是( )
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
5.若

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
5. 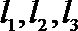
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
12.给出下列关于互不相同的直线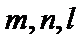
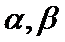
①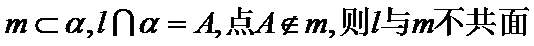
②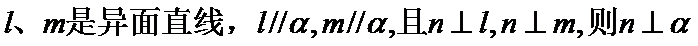
③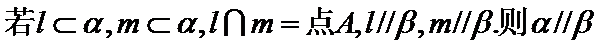
④
其中真命题是_____________(填序号)
正确答案
①②③
解析
解析已在路上飞奔,马上就到!
知识点
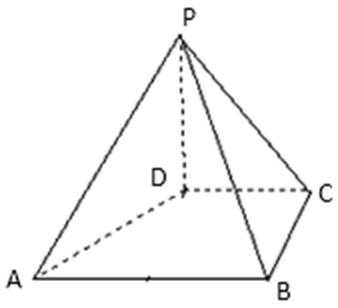
19. 如图,在四棱锥P-ABCD中,PD⊥平面ABCD,PD=DC=BC=1,AB=2,AB∥DC,∠BCD=90°。
(1)求证:PC⊥BC;
(2)求点A到平面PBC的距离。
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
扫码查看完整答案与解析