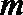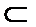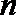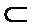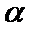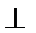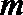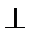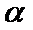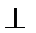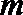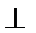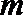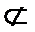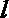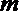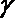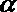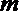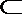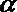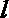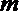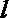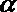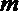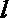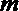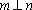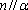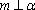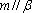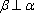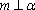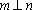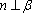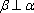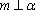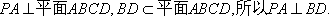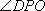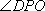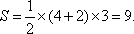- 立体几何与空间向量
- 共2637题
5.


正确答案
解析
根据充分条件和必要条件的定义结婚空间直线的位置关系,进行则l1,l2可能是平行或异面直线,即必要性不成立,
故p是q的充分条件,但不是q的必要条.
考查方向
解题思路



易错点
粗心选错。
知识点
3.已知空间两条不同的直线


正确答案
解析
对于A:正确
对于B:正确应该是
对于C:
对于D:
考查方向
解题思路
本题属于常规题,可使用排除法解答,
易错点
该题易错于对判定定理不熟导致判断失误
知识点
9.已知


①若

②若

③若

④若

其中正确的命题是(填上所有正确命题的序号)( ).
正确答案
① ④
解析
解析已在路上飞奔,马上就到!
知识点
6.已知异面直线a、b分别在平面

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
6.已知直线



①若


②若


③若


④若


其中真命题的个数为( )
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
16.设

①若


②若
③若
④若
其中正确命题的序号是______________(把所有正确命题的序号都写上).
正确答案
①④
解析
解析已在路上飞奔,马上就到!
知识点
7.已知




正确答案
解析
解析已在路上飞奔,马上就到!
知识点
3.直线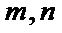
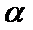
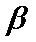
①若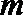
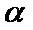
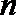

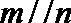
②若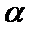
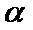
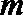
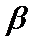
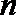
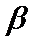
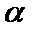
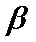
③若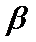
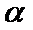
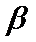
④若
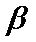
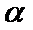
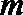

其中正确命题的个数是( )
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
6.设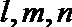
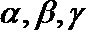
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
6.若直线








正确答案
解析
若直线











知识点
设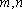
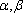
正确答案
解析
对A,若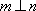
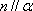

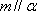
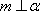
对B,若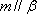
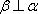

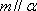

对C,若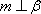
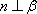
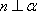
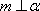
对D,若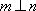
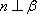
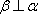
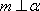

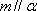
故选C. 点评:本题考查空间中的线线、线面、面面的闻之关系,容易题
知识点
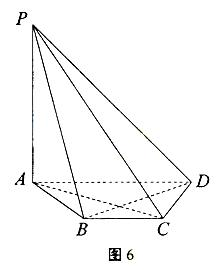
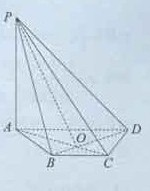
如图6,在四棱锥P-ABCD中,PA⊥平面ABCD,底面ABCD是等腰梯形,AD∥BC,AC⊥BD.
(1)证明:BD⊥PC;
(2)若AD=4,BC=2,直线PD与平面PAC所成的角为30°,求四棱锥P-ABCD的体积.
正确答案
见解析
解析
(1)因为
又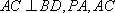
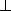
而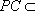
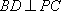
(2)
设AC和BD相交于点O,连接PO,由(1)知,BD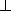
所以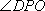
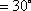
由BD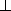

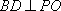
在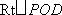
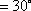
因为四边形ABCD为等腰梯形,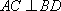
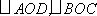
从而梯形ABCD的高为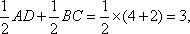
在等腰三角形AOD中,
所以
故四棱锥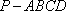
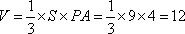
知识点
已知正四棱柱






正确答案
解析
因为底面的边长为2,高为













知识点
如图在直菱柱ABC-A1B1C1中,∠BAC=90°,AB=AC=
(1)证明:AD⊥C1E;
(2)当异面直线AC,C1E 所成的角为60°时,求三菱子C1-A2B1E的体积
正确答案
见解析
解析
(1)


(2)

知识点
已知









正确答案
解析
略
知识点
扫码查看完整答案与解析