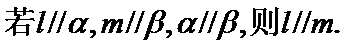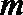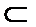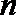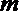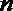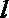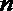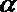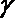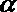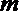- 立体几何与空间向量
- 共2637题
8.用a,b,c表示三条不同的直线,γ表示平面,给出下列命题:
①若a∥b,b∥c,则a∥c;
②若a⊥b,b⊥c,则a⊥c;
③若a∥γ,b∥γ,则a∥b;
④若a⊥γ,b⊥γ,则a∥b.
其中真命题的序号是( )
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
7. 设

①
②
③
④
其中正确命题的个数有( )
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
9.已知


①若

②若

③若

④若

其中正确的命题是(填上所有正确命题的序号)( ).
正确答案
① ④
解析
解析已在路上飞奔,马上就到!
知识点
5.若

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
6.已知直线



①若


②若


③若


④若


其中真命题的个数为( )
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
如图,在三棱锥









(1)求证:

(2)求证:
(3)求三棱锥
正确答案
见解析
解析
(1)因为



所以

又



所以

(2)连结
因为


所以
又



所以


(3)因为平面


所以

所以
知识点
如图,









(1)证明:
(2)证明:
(3)求四棱锥

正确答案
见解析。
解析
(1)证明:连结









(2)证明:





又



由


所以
(3)解:由题




因



∴



则



知识点
下列命题:
①如果一个平面内有一条直线与另一个平面内的一条直线平行,那么这两个平面平行;
②如果一个平面内的两条直线分别平行于另一个平面,那么这两个平面平行;
③平行于同一平面的两个不同平面相互平行;
④垂直于同一直线的两个不同平面相互平行。
其中真命题的是 。
正确答案
解析
略
知识点
如图,在四棱锥E-ABCD中,底面ABCD为正方形, AE⊥平面CDE,已知AE=3,DE=4。
(1)若F为DE的中点,求证:BE//平面ACF;
(2)求直线BE与平面ABCD所成角的正弦值。
正确答案
见解析。
解析
(1)设AC与BD相交于G,连结GF。
正方形ABCD,





(2)解法一:过E点作EH⊥AD,垂足为H,连结BH1分








所以
Rt




解法二:









设直线BE与平面ABCD所成角为
所以直线BE与平面ABCD所成角的正弦值为
知识点
12.给出下列关于互不相同的直线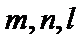
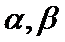
①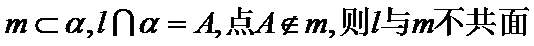
②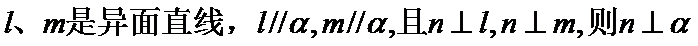
③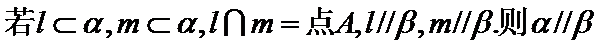
④
其中真命题是_____________(填序号)
正确答案
①②③
解析
解析已在路上飞奔,马上就到!
知识点
16.设

①若


②若
③若
④若
其中正确命题的序号是______________(把所有正确命题的序号都写上).
正确答案
①④
解析
解析已在路上飞奔,马上就到!
知识点
7.已知




正确答案
解析
解析已在路上飞奔,马上就到!
知识点
3.直线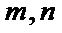
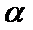
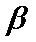
①若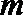
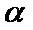
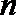

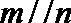
②若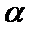
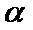
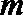
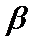
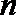
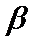
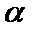
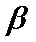
③若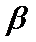
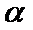
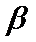
④若
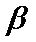
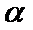
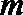

其中正确命题的个数是( )
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
6.设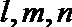
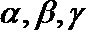
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
2.两个面垂直,经过第一个面内一点且垂直于交线的直线( )
正确答案
解析
因为经过第一个面内一点且垂直于交线的直线有三种情况,分别是与第二个平面垂直、相交、平行,所以选D.
知识点
扫码查看完整答案与解析