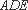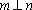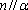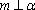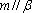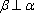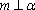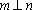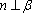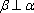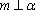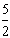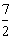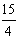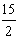- 立体几何与空间向量
- 共2637题
如图,在直三棱柱
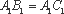

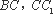


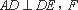

求证:(1)平面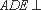
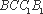
(2)直线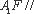

正确答案
见解析
解析
(1)∵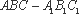

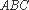
又∵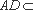
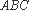
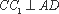
又∵
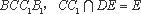
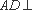
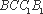
又∵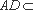
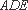
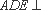
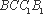
(2)∵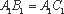
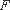
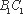
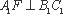
又∵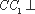
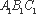
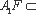
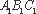
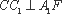
又∵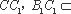

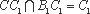
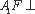
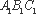
由(1)知,
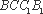
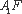
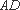
又∵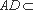
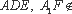
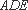

知识点
如图,直三棱柱ABC-A′B′C′,∠BAC=90°,AB=AC=λAA′,点M,N分别为A′B和B′C′的中点。
(1)证明:MN∥平面A′ACC′;
(2)求三棱锥A′-MNC的体积。
(锥体体积公式V=
正确答案
见解析
解析
(1)证法一:连结AB′,AC′,由已知∠BAC=90°,AB=AC,三棱柱ABC-A′B′C′为直三棱柱,
所以M为AB′中点。
又因为N为B′C′的中点,
所以MN∥AC′。
又MN

因此MN∥平面A′ACC′。
证法二:取A′B′中点P,连结MP,NP,
而M,N分别为AB′与B′C′的中点,
所以MP∥AA′,PN∥A′C′,
所以MP∥平面A′ACC′,
PN∥平面A′ACC′。
又MP∩NP=P,
因此平面MPN∥平面A′ACC′。
而MN
因此MN∥平面A′ACC′。
(2) (2)解法一:连结BN,由题意A′N⊥B′C′,平面A′B′C′∩平面B′BCC′=B′C′,所以A′N⊥平面NBC。
又A′N=
故VA′-MNC=VN-A′MC=


解法二:VA′-MNC=VA′-NBC-VM-NBC=
知识点
设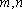
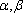
正确答案
解析
对A,若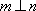
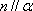

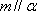
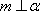
对B,若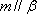
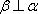

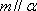

对C,若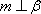
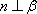
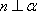
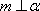
对D,若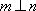
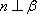
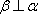
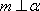

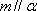
故选C. 点评:本题考查空间中的线线、线面、面面的闻之关系,容易题
知识点
如图,在四棱锥P-ABCD中,AB∥CD,AB⊥AD,CD=2AB,平面PAD⊥平面ABCD,PA⊥AD.E和F分别是CD和PC的中点。
求证:
(1)PA⊥底面ABCD;
(2)BE∥平面PAD;
(3)平面BEF⊥平面PCD.
正确答案
见解析
解析
(1)因为平面PAD⊥底面ABCD,且PA垂直于这两个平面的交线AD,
所以PA⊥底面ABCD.
(2)因为AB∥CD,CD=2AB,E为CD的中点,
所以AB∥DE,且AB=DE.
所以ABED为平行四边形。
所以BE∥AD.
又因为BE

所以BE∥平面PAD.
(3)因为AB⊥AD,而且ABED为平行四边形,
所以BE⊥CD,AD⊥CD.
由(1)知PA⊥底面ABCD,所以PA⊥CD.
所以CD⊥平面PAD.所以CD⊥PD.
因为E和F分别是CD和PC的中点,
所以PD∥EF.所以CD⊥EF.
所以CD⊥平面BEF.
所以平面BEF⊥平面PCD.
知识点
关于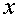
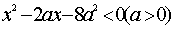
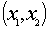
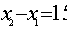
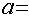
正确答案
解析
∵由x2-2ax-8a2<0(a>0),得(x-4a)(x+2a)<0,即-2a<x<4a,∴x1=-2a,x2=4a.
∵x2-x1=4a-(-2a)=6a=15,
∴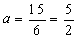
知识点
设集合A={


正确答案
解析

知识点
设m,n是两条不同的直线,α,β是两个不同的平面( )。
正确答案
解析
A选项中直线m,n可能平行,也可能相交或异面,直线m,n的关系是任意的;B选项中,α与β也可能相交,此时直线m平行于α,β的交线;D选项中,m也可能平行于β.故选C
知识点
设





正确答案
解析
知识点
如图,在四棱锥







(1)当正视图方向与向量

(2)若


(3)求三棱锥
正确答案
见解析
解析
本小题主要考查直线与直线、直线与平面的位置关系及几何体的三视图和体积等基础知识,考查空间想象能力,推理论证能力,运算求解能力,考查数形结合能力、化归与转化思想。
解法一:
(1)在梯形



由已知得,四边形
在



又由

从而在


正视图如图所示:
(2)取


在中,是中点,
∴,,又,
∴
∴四边形
又


∴
(3)
又

解法二:
(1)同解法一
(2)取


在梯形

∴四边形为平行四边形
∴,又平面,平面
∴





∴


∴平面


∴
(3)同解法一
知识点
如图,在底面是菱形的四棱锥





(1)求证:

(2)求证:平面

(3)求二面角
正确答案
见解析。
解析
(1)连接BD,交AC于点O,连接OE,在三角形BDP中,







(2)


又








(3)过点



由(2)知,







易得:
知识点
如图,在四棱锥





(1)求证:

(2)求证:

平面


正确答案
见解析
解析
(1)证明:因为底面

又因为 





(2)证明:因为 

又因为 




又因为 


(3)解:如图,连接BD交NC于点F,在平面SNC中过F作

因为 



又因为 



在矩形




所以



知识点
如图,在直角梯形ABEF中,BE∥AF,∠FAB=90°,CD∥AB,将DCEF沿CD折起,使∠FDA=60°,得到一个空间几何体。
(1)求证:BE∥平面ADF;
(2)求证:AF⊥平面ABCD;
(3)求三棱锥E-BCD的体积。
正确答案
见解析。
解析
(1)
由已知条件可知






同理

又




又

∴

(2)由于






(3)法一:


又


法二:取


由(2)易知





又





知识点
如图,已知





的中点。
(1)求证:

(2)求证:平面BCE⊥平面
(3)求此多面体的体积
正确答案
见解析。
解析
(1)取CE中点P,连结FP、BP,∵F为CD的中点, ∴FP∥DE,且FP=
又AB∥DE,且AB=
∴ABPF为平行四边形,∴AF∥BP,
又∵AF

(2)∵
∵AB⊥平面ACD,DE//A

∴DE⊥AF 又AF⊥CD,CD∩DE=D
∴AF⊥平面
又∵BP
(3)此多面体是一个以C为定点,以四边形ABED为底边的四棱锥,


知识点
如图,已知四棱锥



且
(1)求证:

(2)求证:

(3)若


正确答案
见解析。
解析
(1)




又

∴
(2)


则
∴



∴
又
∴
(3)在直角梯形



则四边形
在

故
∵

∴



∴
知识点
已知




正确答案
解析
略
知识点
扫码查看完整答案与解析