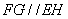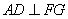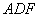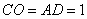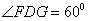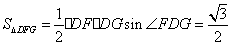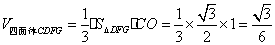- 立体几何与空间向量
- 共2637题
如图5,AB是圆O的直径,点C是弧AB的中点,点V是圆O所在平面外一点,


(1)求证:OD//平面VBC;
(2)求证:AC⊥平面VOD;
(3)求棱锥
正确答案
见解析。
解析
(1)∵ O、D分别是AB和AC的中点,∴OD//BC .
又

(2)∵VA=VB,O为AB中点,∴
连接



∴


∵


∵

又∵



∵VO平面VOD,VD平面VOD,

(3)由(2)知


又∵点C是弧的中点,∴

∴三角形

∴棱锥

故棱锥

知识点
某工厂准备对已编号(1~60)的60件产品,采用系统抽样的方法欲选取6件产品进行抽样试验,那么选取的产品编号可能是:
正确答案
解析
略
知识点
下列函数中,既是偶函数,又是在区间
正确答案
解析
略
知识点
如图,已知三棱锥A—BPC中,AP⊥PC,AC⊥BC,M为AB中点,D为PB中点,且△PMB为正三角形。
(1)求证:DM//平面APC;
(2)求 证:平面ABC⊥平面APC;
(3)若BC=4,AB=20,求三棱锥D—BCM的体积。
正确答案
见解析。
解析
知识点
如图1,在Rt△ABC中,∠ABC=90°,D为AC中点,




(1)若M是FC的中点,求证:直线

(2)求证:BD⊥
(3)若平面


正确答案
见解析
解析
(1)因为




又
所以
(2)因为

所以
又
所以
(3)直线

因为



所以 
因为

又因为

假设
因为

所以
所以
这与
所以直线

知识点
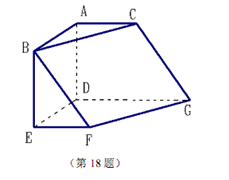
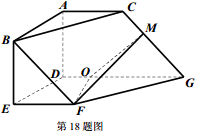
如图










(1)求证:

(2)求证:

(3)求五面体
正确答案
见解析。
解析
(1)证明:连接






∵

∴


∵





∴

∵
∴


∴四边形
∴


∵



∴

(2)证法1:取



由(1)知,


∴四边形
∴


在Rt△



∴
在△



∴
∴
∴

∵四边形
∴
∵




∴

证法2:在Rt△


∴
在△

∴
∴
∵

∴
∵




∴

∵

∴
∵四边形
∴
∵




∴

(3)
解:连接
在Rt△

∴
由(2)知



∴

∵



∴

∴四棱锥

∴三棱锥

∴五面体

知识点
已知函数:



正确答案
解析
知识点
甲、乙进行乒乓球比赛,比赛规则:在一局比赛中,先得11分的一方为胜方,10平后,先得2分的一方为胜方。
(1)根据以往战况,双方在每一分的争夺中甲胜的概率为
(2)在五局比赛中,记甲以8∶9落后的情况下最终以12∶10获胜的局数为

正确答案
见解析。
解析
(1)比分从8:9到12:10只有以下三种情况:
由此可以看出,最后两分必是甲得分且必出现10平,所以甲以8:9落后的情况下最终以12:10获胜的概率为
故甲以8:9落后的情况下最终以12:10获胜的概率为
(2)因为

故

知识点
如图,已知直三棱柱




(1)求证:

(2)求证:
正确答案
见解析
解析
(1)证明:连接


∵



∴
∵



∴

(2)连接


∵



∴
∵



∴
知识点
如图,在三棱柱










(3)求三棱锥
正确答案
见解析。
解析
证明:






(2)证明:在



满足

又因为四边形
又
又因为
又因为四边形


(3)解:
过







知识点
已知四面体P—ABCD中,PB



(1)求证:平面PAD
(2)当Q在什么位置时,PA∥平面QBD?
正确答案
见解析。
解析
知识点
如图,四棱锥







(1)证明:

(2)证明:
正确答案
见解析。
解析
(1)因为



所以

因为


所以

(2)因为
所以
因为
又因为

所以
所以
得

因为

所以
知识点
在下图的几何体中,面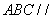
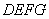
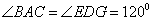
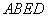
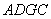
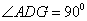
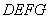
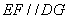
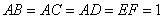
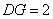
(1)求证: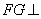
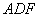
(2)求四面体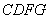
正确答案
见解析。
解析
(1)连接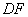
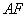
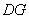
∵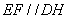
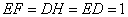
∴四边形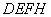
∴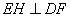
又∵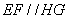
∴四边形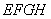
∴
∴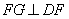
由已知条件可知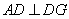
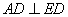
所以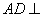
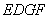
又∵
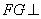
(2)取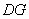
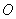
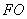
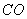
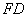
因为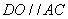
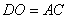
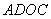
所以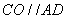
由第一问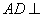
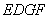
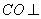
由已知,可知在三角形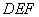
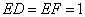
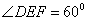
所以有正三角形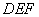
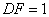
知识点
如图5,在平行四边形ABCD中,∠A=90°,∠B=135°,∠C=60°,AB=AD,M,N分别是边AB,CD上的点,且2AM=MD,2CN=ND,如图5,将△ABD沿对角线BD折叠,使得平面ABD⊥平面BCD,并连结AC,MN(如图6)。
(1)证明:MN∥平面ABC;
(2)证明:AD⊥BC;
(3)若BC=1,求三棱锥A-BCD的体积。
正确答案
见解析。
解析
知识点
执行如图所示的程序框图,输出的x值为()
正确答案
解析
略
知识点
扫码查看完整答案与解析