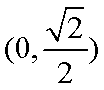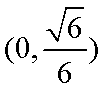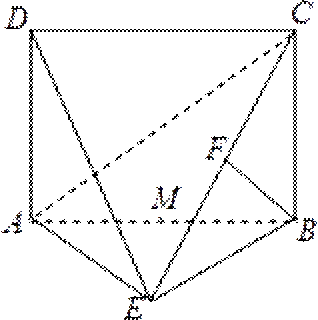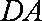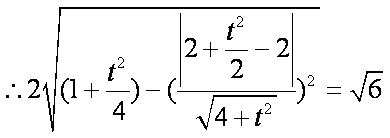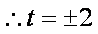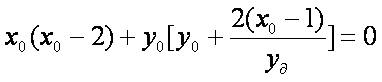- 立体几何与空间向量
- 共2637题
如图所示,平面





(1)求证:

(2)求三棱锥
正确答案
见解析。
解析
(1)
证明:

又∵ABCD为正方形,∴BC//AD,∴BC//EF。 …………4分
又

(2)∵平面PAD⊥平面ABCD,CD⊥AD,∴CD⊥平面PAD,即GD⊥平面AEF。 ……8分
又∵EF//AD,PA⊥AD,∴EF⊥AE。 …………10分
又

知识点
如图,在梯形









(1)求证:

(2)当


正确答案
见解析。
解析
(1)由题意知,


所以
又平面



所以

(2)当


在梯形



因为

所以

所以四边形
所以
又



所以

知识点
定义域为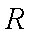







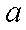
正确答案
解析
试题分析: 由

又
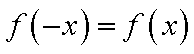

即

设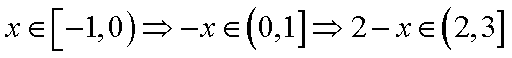
由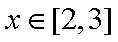
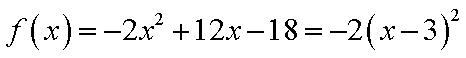
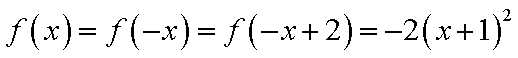
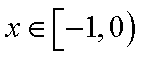

易得
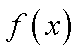
若满足函数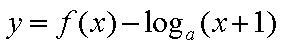
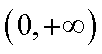

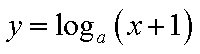
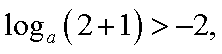

知识点
如图,四边形


(1) 求证:
(2) 求证:平面
(3) 求体积

正确答案
见解析。
解析
(1)
设BD交AC于M,连结ME.
∵ABCD为正方形,所以M为AC中点,
又∵E为

∴
∴
(2)∵ABCD为正方形 ∴
∵
又
∵
∴
(3)
知识点








正确答案
见解析。
解析
(1)由













知识点
如图:四棱柱


(1)证明:
(2)求点

正确答案
见解析
解析
解析:(1)证明:过



在



在








(2)三棱锥

在
同理,
因此
设点





知识点
如图,四边形
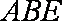
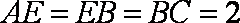
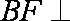
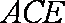
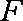
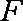
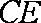
(1)求证:
(2)求四棱锥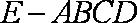
(3)设点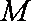
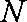
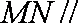
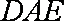
正确答案
见解析。
解析
(1)因为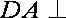
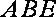
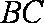
所以
因为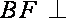
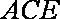
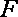

因为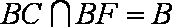
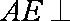
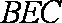
则
因为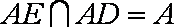
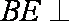
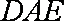
则

(2)
作

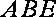
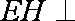
因为
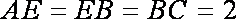
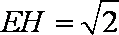

(3)因为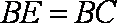
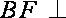
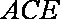
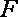
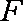
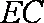
设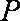
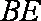
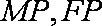
所以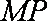
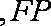
因为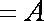
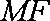
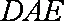
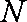
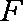
知识点
已知椭圆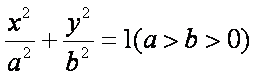
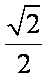
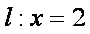
(1)求椭圆
(2)设O为坐标原点,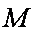
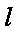
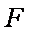

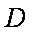
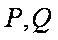
①若
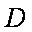
②若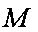
正确答案
见解析
解析
(1)由题设: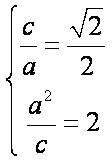

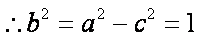


(2)①由(1)知: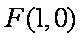
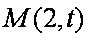
则圆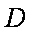
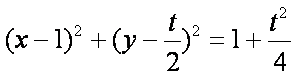
直线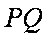
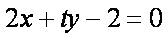
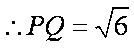
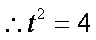
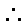
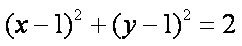
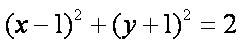
②解法(一):设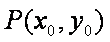
由①知: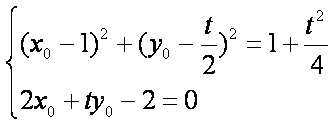
即: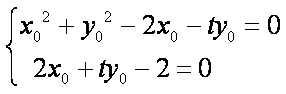
消去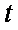
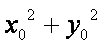
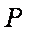
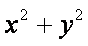
解法(二):设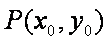
则直线FP的斜率为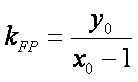
∵FP⊥OM,∴直线OM的斜率为
∴直线OM的方程为:
点M的坐标为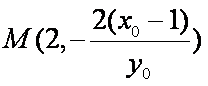
∵MP⊥OP,∴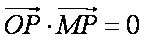
∴
∴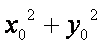

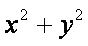
知识点
四棱锥






(1)求证:
(2)在



(3)求三棱锥
正确答案
见解析
解析
(1)证明:连接AC, 
由余弦定理得

取





(2)当




证明:取














(3)















知识点
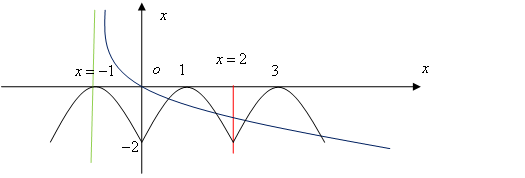
执行如图所示的程序框图,若输出的结果为63,则判断框中应填
正确答案
解析
略
知识点
如图
正确答案
解析
初始值















知识点
函数 


正确答案
解析
略
知识点
如图,将边长为2的正方形








(1)求证:

(2)求证:

(3)求三棱锥
正确答案
见解析
解析
解析:(1)在正方形

∵平面


∴




(2)
分别取



则

又

∴四边形
∴
∵

又



(3)∵


∴
知识点
稿酬所得以个人每次取得的收入,定额或定率减除规定费用后的余额为应纳税所得额,每次收入不超过4000元,定额减除费用800元;每次收入在4000元以上的,定率减除20%的费用.适用20%的比例税率,并按规定对应纳税额减征30%,计算公式为:
(1)每次收入不超过4000元的:应纳税额=(每次收入额-800)×20%×(1-30%)
(2)每次收入在4000元以上的:应纳税额=每次收入额×(1-20%)×20%×(1-30%).
已知某人出版一份书稿,共纳税280元,这个人应得稿费(扣税前)为 元。
正确答案
答案:2800
解析
略
知识点
如图,正三棱柱ABC-A1B1C1中,底面边长为2,侧棱长为
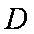

(1)求证;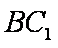
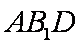
(2)三棱锥
正确答案
见解析。
解析
(1)如图,连结A1B与AB1交于E,连结DE,则E为A1B的中点,
∴BC1∥DE, 


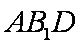
∴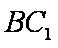

(2)过点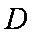


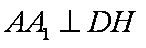
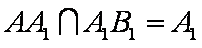
∴
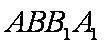

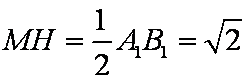
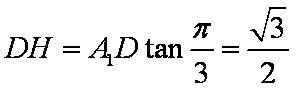
∵
知识点
扫码查看完整答案与解析