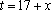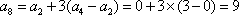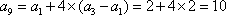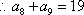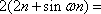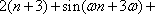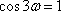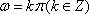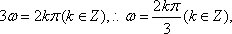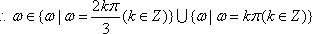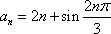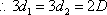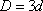- 立体几何与空间向量
- 共2637题
请你谈一谈对“不同生产方式以及生产工艺中,生产物流管理所采用的方法和手段是不同的。”这句话的理解。
正确答案
测试
三棱柱





(1)求证:

(2)求证:

(3)求三棱锥
正确答案
见解析。
解析
⑴连结





又∵



⑵∵三棱柱


∴











⑶由⑵知



∴


知识点
如图,四棱锥



(1)求证:
(2)求证:
正确答案
;见解析。
解析
(1)连接AC交BE于点O,连接OF,不妨设AB=BC=1,则AD=2

又
(2)


知识点
若实数x,y满足不等式组 2x +y -7≥0,则3x+4y的最小值是
x≥0,y≥0
正确答案
解析
略
知识点
设抛物线C:y2=4x的焦点为F,直线l过F且与C交于A,B两点,若|AF|=3|BF|,则l的方程为( )。
正确答案
解析
由题意可得抛物线焦点F(1,0),准线方程为x=-1.
当直线l的斜率大于0时,如图所示,过A,B两点分别向准线x=-1作垂线,垂足分别为M,N,则由抛物线定义可得,|AM|=|AF|,|BN|=|BF|。
设|AM|=|AF|=3t(t>0),|BN|=|BF|=t,|BK|=x,而|GF|=2,
在△AMK中,由

解得x=2t,则cos∠NBK=
∴∠NBK=60°,则∠GFK=60°,即直线AB的倾斜角为60°。
∴斜率k=tan 60°=

当直线l的斜率小于0时,如图所示,同理可得直线方程为y=
知识点
如图, 四棱柱ABCD-A1B1C1D1的底面ABCD是正方形, O为底面中心, A1O⊥平面ABCD, 
(1) 证明: A1BD // 平面CD1B1;
(2)求三棱柱ABD-A1B1D1的体积.
正确答案
见解析
解析
(1) 设


(2) 
在正方形AB CD中,AO = 1 .

所以,
知识点
若行列式
正确答案
2
解析
略
知识点
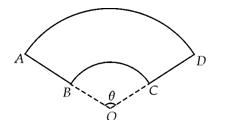
某公司承建扇环面形状的花坛如图所示,该扇环面花坛是由以点
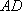
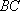
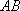
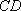
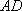
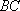

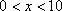
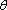
(1)求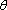

(2)在对花坛的边缘进行装饰时,已知两条线段的装饰费用为4元/米,两条弧线部分的装饰费用为9元/米.设花坛的面积与装饰总费用的比为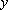

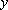
正确答案
(1)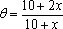
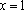
解析
(1)设扇环的圆心角为,则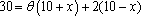
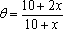
(2) 花坛的面积为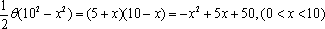
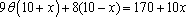
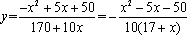
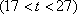
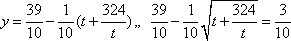
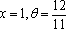
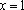
知识点
如图,直三棱柱ABC-A1B1C1中,D,E分别是AB,BB1的中点。
(1)证明:BC1∥平面A1CD;
(2)设AA1=AC=CB=2,AB=
正确答案
见解析
解析
(1)连结AC1交A1C于点F,则F为AC1中点。
又D是AB中点,连结DF,则BC1∥DF.
因为DF⊂平面A1CD,BC1
所以BC1∥平面A1CD.
(2)因为ABC-A1B1C1是直三棱柱,所以AA1⊥CD.
由已知AC=CB,D为AB的中点,所以CD⊥AB.
又AA1∩AB=A,于是CD⊥平面ABB1A1.
由AA1=AC=CB=2,



故A1D2+DE2=A1E2,即DE⊥A1D.
所以VC-A1DE=
知识点
已知




正确答案
解析
略
知识点
设a,b,c为单位向量,a,b的夹角为600,则(a + b + c)·c的最大值为 。
正确答案
解析
略
知识点
已知




正确答案
2
解析
略
知识点
若数列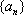

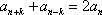
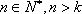
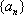
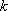
(1)已知数列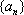
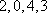
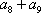
(2)若
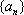
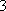
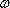
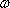
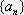

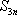
(3)若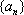
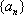
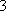
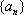
正确答案
见解析
解析
(1)
(2)


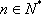
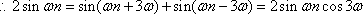
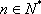
所以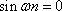
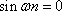
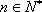
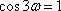
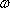
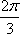
由于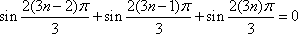
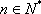

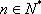
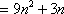
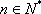
(3)若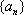
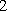
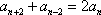
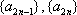
设等差数列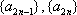
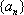
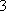
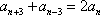

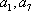
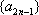
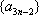
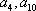

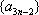
设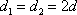
所以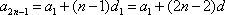
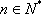
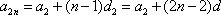
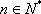
又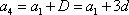

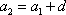
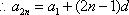
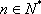
综合得: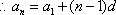
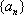
知识点
如图,四棱锥P—ABCD中,底面ABCD是菱形,PA= PD,
(1)求证:AD
(2)若Q是PC的中点,求证:PA∥平面BDQ;
(3)若

正确答案
见解析。
解析
(1)证明:
由E是AD的中点, PA=PD,所以AD⊥PE;
又底面ABCD是菱形,∠BAD=60
所以AB=BD,又因为E是AD的中点 ,
所以AD⊥BE,
又PE∩BE=E 所以AD⊥平面PBE.
(2)证明:连接AC交BD于点O,连OQ;因为O是AC的中点,
Q是PC的中点,所以OQ//PA,
又PA

(3)解:设四棱锥P-BCDE,Q-ABCD的高分别为
所以

又因为

所以
知识点
如图,四棱柱ABCD-A1B1C1D1的底面ABCD是正方形,O为底面中心,A1O⊥平面ABCD,
(1)证明:A1BD // 平面CD1B1;
(2)求三棱柱ABD-A1B1D1的体积,
正确答案
见解析
解析
知识点
扫码查看完整答案与解析