- 立体几何与空间向量
- 共2637题
如图1,在直角梯形



现以







(1)求证:

(2)求证:
(3)求点

正确答案
见解析。
解析
(1)证明:
取


在△


所以


由已知


所以


所以四边形
所以

又因为



所以

(2)在正方形

又因为平面



所以

所以
在直角梯形



在△

所以
所以
所以

(3)解法一:因为



过点




所以点


在直角三角形
所以
所以点


解法二:

所以
又


则 
所以点


知识点
已知直线m、n和平面α,在下列给定的四个结论中,m∥n的一个必要但不充分条件是
正确答案
解析
略
知识点
三棱锥







正确答案
解析
在△

















知识点
在直三棱柱




正确答案
解析
如图,取



























知识点
如图5,已知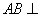
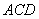
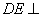
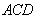
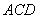
三角形,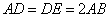
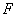
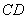
(1)求证: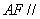
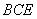
(2)求证:平面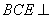
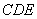
正确答案
见解析。
解析
证明:(1) 证:取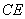
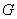
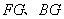
∵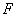
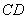
∴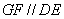

∵
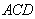
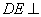
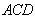
∴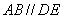
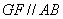
又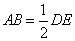
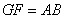
∴四边形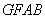
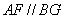
∵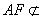
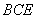
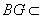
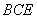
∴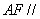
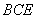
(2)求证:平面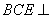
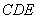
证:∵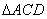
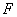
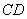
∴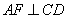
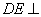
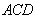
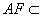
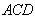
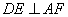
又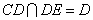
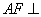
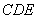
∵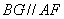
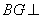
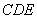
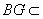
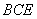
∴平面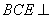
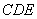
知识点
设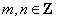
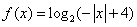
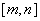

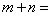
正确答案
解析
由题意,当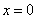
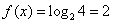
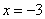
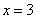
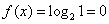

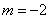
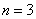
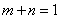
知识点
设a,b,c是空间三条直线,
正确答案
解析
略
知识点
已知
正确答案
解析
略
知识点
如图,正方体ABCD-A1B1C1D1的棱长为4,点P、Q在棱CC1上,PQ=1,


正确答案
解析
如图,连接


































知识点
如图,四边形ABCD为矩形,

(1)求证ED
(2)求四棱锥E—ABCD的体积;
(3)设点M在线段AB上,且AM=MB,试在线段CE上确定一点N,使得MN//平面DAE.
正确答案
见解析。
解析
知识点
如图1,直角梯形








(1) 证明:

(2) 求三棱锥
正确答案
见解析。
解析
(1)证明:取

















又因为



所以

(2)面



面



又

梯形



所以,



又


作



在直角三角形

所以,
另解:









因为翻折后垂直关系不变,所以



面










知识点
直三棱柱 




(1)求证:BP∥平面ACD,
(2)求证:平面
正确答案
见解析。
解析
知识点
将棱长为




(1)证明:
(2)求三棱锥
正确答案
见解析。
解析
(1)证:连接

∵


∴
∵点



又∵
∴

又∵
∴
∴
又∵
∴
又∵
∴
(2)解:∵



∵点



∴
∴
知识点
在三棱锥






(1)求证:

(2)求证:

(3)求三棱锥
正确答案
见解析。
解析
(1)


又


∴

(2)
如图,连结




∴


同理, 


又
∴
∴
∴








(3)由(2)可知
∴

∴
知识点
如图,在四棱锥



(1)若





(2)求证:
(3)若


正确答案
见解析
解析
(1)如图,连结
因为底面
所以

又因为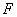

所以

在△




所以

又因为



所以

(2)因为平面



又


所以

又因为

所以

(3)在△

所以
由(2)可知

所以

又因为
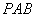
所以平面

知识点
扫码查看完整答案与解析