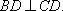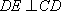- 立体几何与空间向量
- 共2637题
已知某个几何体的三视图如图所示,则这个几何体的体积是 。
正确答案
6
解析
由已知中的三视图可得
该几何体是一个以俯视图为底面,
以2为高的四棱锥
故这个几何体的体积V=

故答案为:6
知识点
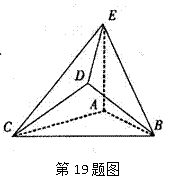
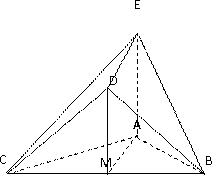
如图,已知平面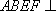
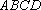
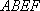

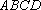
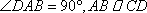
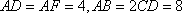
(1)求证: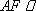
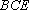
(2)求证: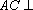
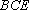
(3)求四棱锥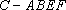
正确答案
见解析
解析
知识点
如图,四边形




(1)求证:
(2)若点




(3)试


正确答案
见解析
解析
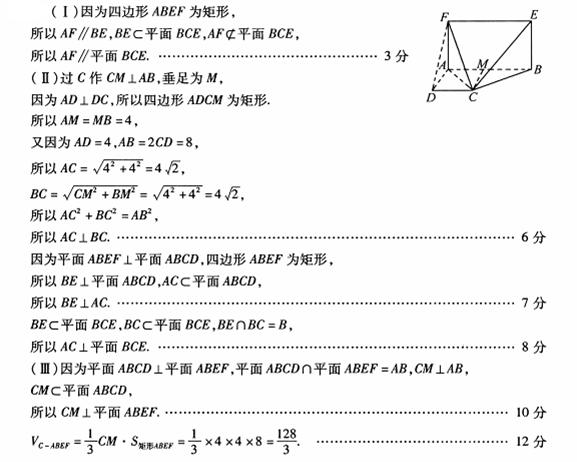
(1)因为



因为


由已知得

所以




所以
(2)过




又

又


.………6分
且

………7分
所以
又



所以

(3)直线

证明如下:
由(1)可知,
在四边形


所以

设

则

又因为


知识点
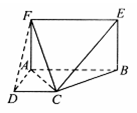
如图,五面体ABCDEF中,点O是矩形ABCD的对角线的交点,面ABF是等边三角形,棱EF//BC,且EF=

(2)若EF=EO,证明:平面EFO
正确答案
见解析。
解析
知识点
如图,正方形ABCD和直角梯形ABMN所在平面相互垂直,AN//BM,∠ABM=90°,AN=AD=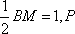
(1)证明NP//面ABCD;
(2)证明:MN⊥NC;
(3)求三棱锥M—BPN的体积.
正确答案
见解析。
解析
知识点
在如图所示的几何体中,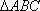
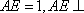
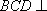
(1)AE//平面BCD;
(2)平面BDE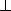
正确答案
见解析
解析
(1)
取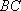
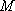
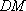
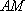
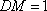
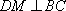
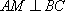
又因为平面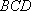
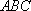
所以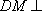
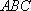
因为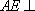
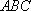
所以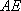
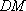
又因为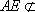
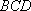
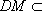
所以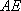
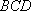
(2)由(1)知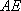
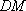
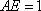
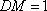
所以四边形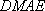
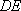
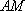
因为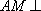
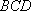
所以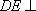
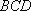
又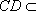
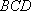
由已知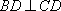
则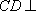
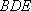
因为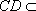
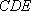
所以平面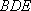
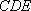
(也可利用勾股定理证明题中的垂直关系.)
知识点
在如图所示的几何体中,四边形









(1)求证:

(2)在



正确答案
见解析
解析
(1)证明:取


在




所以
又因为
所以

所以四边形
所以
又因为



故

(2)解:假设在


因为


又因为


在

因为



显然,当

因为



易得

所以

知识点
如图1所示,在Rt△ABC中,AC =6,BC =3,∠ABC= 
(1)求证:DE⊥平面BCD;
(2)若EF∥平面BDG,其中G为直线AC与平面BDG的交点,求三棱锥
正确答案
见解析。
解析
(1)在图1中,因为AC=6,BC=3,所以

因为CD为∠ACB的角平分线,所以

因为CE=4,

即
则

在图2中,因为平面BCD⊥平面ACD,平面BCD

(2)
在图2中,因为EF∥平面BDG,EF
平面ABC
因为点E在线段AC上,CE=4,点F是AB的中点,
所以AE=EG=CG=2,(8分)
作BH⊥CD于点H,因为平面BCD⊥平面ACD,
所以BH⊥平面ACD。
由已知可得

所以三棱锥

知识点
已知直线m,l,平面α,β,且m⊥α,l⊂β,给出下列命题:
①若α∥β,则m⊥l;②若α⊥β,则m∥l;
③若m⊥l,则α∥β④若m∥l,则α⊥β
其中正确命题的个数是( )
正确答案
解析
(1)中,若α∥β,且m⊥α⇒m⊥β,又l⊂β⇒m⊥l,所以①正确。
(2)中,若α⊥β,且m⊥α⇒m∥β,又l⊂β,则m与l可能平行,可能异面,所以②不正确。
(3)中,若m⊥l,且m⊥α,l⊂β⇒α与β可能平行,可能相交,所以③不正确。
(4)中,若m∥l,且m⊥α⇒l⊥α又l⊂β⇒α⊥β,∴④正确,故选B。
知识点
如图,在四棱锥P—ABCD中,平面

求证:(1)直线EF//平面PBC;
(2)平面DEF
正确答案
见解析。
解析
知识点
如图,矩形





(1)求证:

(2)求证:

(3)求三棱锥
正确答案
见解析。
解析
(1)证明:∵





又∵


∵
(2)证明:连结


∵





∴
∵


(3)解:取



∵


∵


∴
故三棱锥
知识点
已知四棱锥


正确答案
解析
可证四个面都是直角三角形,其面积
知识点
正三棱柱ABC﹣A1B1C1中,AB=2,D是AC中点,且AB1⊥BC1
(1)求侧棱AA1的长;
(2)求二面角D﹣BC1﹣C的余弦值。
正确答案
见解析。
解析
(1)取A1B1中点E,连接BC1,EC1,可得△ABB1∽△BB1E,从而可求侧棱AA1的长;
(2)过D做DO⊥BC,垂足为O,过O做OG⊥BC1,垂足为G,连接DG,则DG⊥BC1,故∠OGD为二面角D﹣BC1﹣C的平面角,计算OD,OG,即可求得结论。
(1)证明:取A1B1中点E,连接BC1,EC1,
∵ABC﹣A1B1C1是正三棱柱,∴AB1⊥EC1
∵AB1⊥BC1,BC1∩EC1=C1,
∴AB1⊥平面BEC1,∴AB1⊥BE
∴△ABB1∽△BB1E
∴
∵AB=2,∴
∴
(2)解:过D做DO⊥BC,垂足为O,过O做OG⊥BC1,垂足为G,连接DG,则DG⊥BC1,
∴∠OGD为二面角D﹣BC1﹣C的平面角
在△CBC1中,由等面积可得OG=
∵OD=
∴∠OGD=45°
∴二面角D﹣BC1﹣C的余弦值为
知识点
设



正确答案
解析
略
知识点
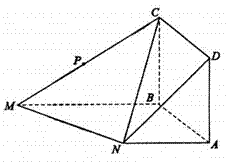
如图(5),已知三棱柱BCF-ADE的侧面CFED与ABFE都是边长
为1的正方形,M 、N两点分别在AF和CE上,且AM=EN。
(1)求证:平面ABCD
(2)求证: MN//平面BCF;
(3)若点N为EC的中点,点P为EF上的动点,试求PA+PN的最小值。
正确答案
见解析。
解析
(1)∵四边形CFED与ABFE都是正方形
∴



又∵

∵

(2)证法一:
过点M作

过点N作


∵
又∵
∴四边形

法二:
过点M作

同理可证得

∵MN

(3)
如图将平面EFCD绕EF旋转到与ABFE在同一平面内,则当点
A、P、N在同一直线上时,PA+PN最小,
在△AEN中,∵
由余弦定理得
∴

知识点
扫码查看完整答案与解析