- 立体几何与空间向量
- 共2637题
过点A(-1,0),斜率为k的直线,被圆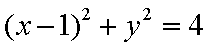
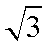
正确答案
解析
试题分析:设直线为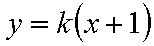
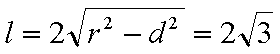
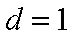
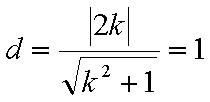
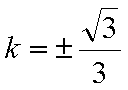
知识点
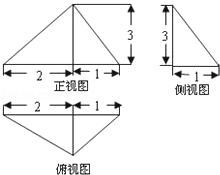
已知某几何体的三视图如图所示,其中正视图,侧视图均是由三角形与半圆构成,视图由圆与内接三角形构成,根据图中的数据可得此几何体的体积为( )
正确答案
解析
由三视图知,原几何体是一个三棱锥和一个半球的组合体,其中三棱锥的一个侧棱垂直于底面等腰直角三角形,且高为1,底面等腰直角三角形的腰为1,球的直径为 
∴原几何体的体积为V=





知识点



正确答案
解析
∵











知识点
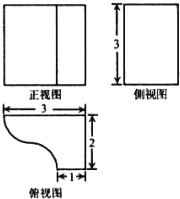
已知某几何体的三视图如图所示,则该几何体的体积为 。
正确答案
解析
由已知中的三视图可得几何体是一个三棱锥
且棱锥的底面是一个以(2+1)=3为底,以1为高的三角形
棱锥的高为3
故棱锥的体积V=

知识点
如图①,已知


(1)证明:DE//平面BCF;
(2)证明:CF
(3)当AD=
正确答案
见解析
解析
(1)在等边三角形


在折叠后的三棱锥







(2)在等边三角形









(3)由(1)可知


知识点
如图,是某几何体的三视图,其中正视图是腰长为2的等腰三角形,俯视图是半径为1的半圆,则该几何体的体积是 。
正确答案
解析
由三视图知,几何体是半个圆锥,
圆锥的底面半径是1,母线长是2,
∴圆锥的高是
∴圆锥的体积是
知识点
如图,三棱柱ABC﹣A1B1C1中,侧棱垂直底面,∠ACB=90°,AC=BC=
(1)证明:平面BDC1⊥平面BDC
(2)平面BDC1分此棱柱为两部分,求这两部分体积的比。
正确答案
见解析。
解析
(1)由题设知BC⊥CC1,BC⊥AC,CC1∩AC=C,
∴BC⊥平面ACC1A1,又DC1⊂平面ACC1A1,
∴DC1⊥BC。
由题设知∠A1DC1=∠ADC=45°,
∴∠CDC1=90°,即DC1⊥DC,又DC∩BC=C,
∴DC1⊥平面BDC,又DC1⊂平面BDC1,
∴平面BDC1⊥平面BDC;
(2)设棱锥B﹣DACC1的体积为V1,AC=1,由题意得V1=


又三棱柱ABC﹣A1B1C1的体积V=1,
∴(V﹣V1):V1=1:1,
∴平面BDC1分此棱柱两部分体积的比为1:1
知识点
一个四棱锥的三视图如图所示,其左视图是等边三角形,该四棱锥的体积= 。
正确答案
解析
试题分析:由题意得几何体为:底面为上底为1,下底为2,高为2的直角梯形,顶点在地面上射影为直角梯形高的中点,即锥的高为
知识点
已知某几何体的三视图如图所示,根据图中标出的尺寸(单位cm),可得这个几何体的体积是 cm3。
正确答案
12
解析
由三视图可知:该几何体可以看成一个棱长为4,2,3的长方体的一半。
∴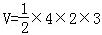
故答案为12。
知识点
设


正确答案
解析
试题分析:由题意得:

知识点
设D、E、F分别是△ABC的三边BC、CA、AB上的点,且

正确答案
解析
由题意,



∵
知识点
在△ABC中,若a=2,∠B=60°,b=
正确答案
解析
∵△ABC中,a=2,b=
∴根据余弦定理,得b2=a2+c2﹣2accosB,
可得7=4+c2﹣4ccos60°,化简得c2﹣2c﹣3=0,解之得c=3(舍负)
∴△ABC的面积S=

又∵△ABC的面积S=
∴h=

知识点
如图,边长为1的菱形OABC中,AC交OB于点D,∠AOC=60°,M,N分别为对角线AC,OB上的点,满足


正确答案
解析
∵边长为1的菱形OABC中,∠AOC=60°,
∴|AC|=1,|OB|=
∴






∴



知识点
已知某几何体的三视图如图所示,则该几何体的体积为 。
正确答案
解析
由已知中的三视图可得几何体是一个三棱锥
且棱锥的底面是一个以(2+1)=3为底,以1为高的三角形
棱锥的高为3
故棱锥的体积V=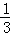
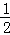
知识点
如图,C,B,D,E四点共圆,ED与CB的延长线交于点A,若AB=4,BC=2,AD=3,则DE= 。
正确答案
5
解析
由割线定理可得:AD•AE=AB•AC,
∵AB=4,BC=2,AD=3,
∴3×(3+DE)=4×(4+2),
解得DE=5。
故答案为5。
知识点
扫码查看完整答案与解析