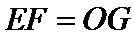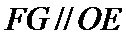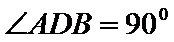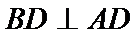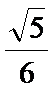立体几何与空间向量_章节学习

1

题型：填空题

|

填空题 · 6 分

9. 某几何体的三视图如图所示（单位：cm），则该几何体的表面积是______cm2,体积是______cm3.

正确答案

80　；40．

考查方向

本题主要考查了三视图等知识，为高考题的必考题，在近几年的各省高考题出现的频率较高

解题思路

先画出立体几何体，再求出图形的表面积和体积

试题分析：由三视图知该组合体是一个长方体上面放置了一个小正方体，

，

易错点

对三视图变成立体几何体存在问题

知识点

平面与平面平行的判定与性质

1

题型：单选题

|

单选题 · 5 分

3.将一个长方形沿相邻三个面的对角线截去一个棱锥，得到的几何体的正视图与俯视图如图所示，则该几何体的侧（左）视图为（）

A

B

C

D

正确答案

B

解析

试题分析：由题意得截去的是长方体前右上方顶点，故选B

考查方向

本题主要考查了三视图，为高考常考题，在近几年的各省高考题出现的频率较高，常与几何体的表面积、体积等知识点交汇命题，由三视图还原出原几何体,是解决此类问题的关键。

解题思路

解答此类题目的关键是由多面体的三视图想象出空间几何体的形状并画出其直观图，三视图中“正侧一样高、正俯一样长、俯侧一样宽”，因此，可以根据三视图的形状及相关数据推断出原几何图形中的点、线、面之间的位置关系及相关数据．本题直接用排除法进行判断即可。

易错点

忽略三视图中线的虚实导致出错。

知识点

平面与平面平行的判定与性质

1

题型：简答题

|

简答题 · 13 分

如图，四边形ABCD是平行四边形，平面AED⊥平面ABCD，EF||AB，AB=2，BC=EF=1，AE=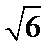，DE=3，∠BAD=60º，G为BC的中点.

19.求证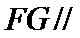：平面BED；

20.求证：平面BED⊥平面AED；

21.求直线EF与平面BED所成角的正弦值.

第(1)小题正确答案及相关解析

正确答案

（Ⅰ）证明：取的中点为，连接，在中，因为是的中点，所以且，又因为，所以且

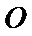
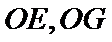
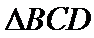
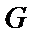
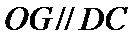
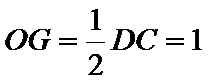
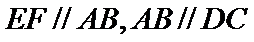
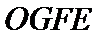
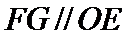
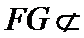
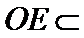
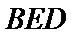
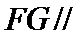
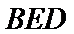
，即四边形是平行四边形，所以，又平面，平面，所以平面.

解析

试题分析：本题属于立体几何的综合应用问题，属于中档题，只要掌握相关立体几何的定理及性质，即可解决本题，解析如下：

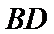
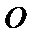
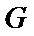
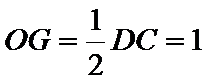
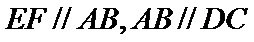
试题解析：（Ⅰ）证明：取的中点为，连接，在中，因为是的中点，所以且，又因为，所以且

，即四边形是平行四边形，所以，又平面，平面，所以平面.

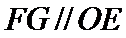
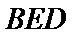
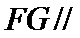
考查方向

本题考查了直线与平面平行和垂直、平面与平面垂直、直线与平面所成角等知识点。

解题思路

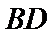
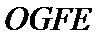
（Ⅰ）证明线面平行，一般利用线面平行判定定理，即从线线平行出发给予证明，而线线平行寻找与论证，往往结合平几知识，如本题构造一个平行四边形：取的中点为，可证四边形是平行四边形，从而得出

易错点

解题步骤不完整或考虑不全致推理片面导致出错。

第(2)小题正确答案及相关解析

正确答案

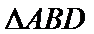
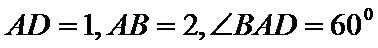
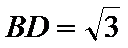
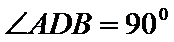
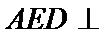
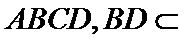
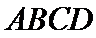
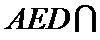
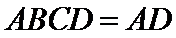
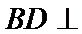
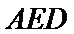
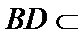
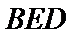
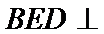
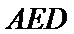
（Ⅱ）证明：在中，，由余弦定理可，进而可得，即，又因为平面平面平面；平面平面，所以平面.又因为平面，所以平面平面.

解析

试题分析：本题属于立体几何的综合应用问题，属于中档题，只要掌握相关立体几何的定理及性质，即可解决本题，解析如下：

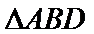
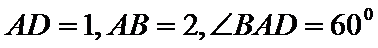
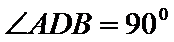
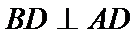
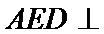
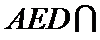
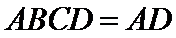
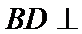
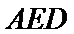
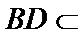
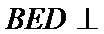
（Ⅱ）证明：在中，，由余弦定理可，进而可得，即，又因为平面平面平面；平面平面，所以平面.又因为平面，所以平面平面.

考查方向

本题考查了直线与平面平行和垂直、平面与平面垂直、直线与平面所成角等知识点。

解题思路

（Ⅱ）面面垂直的证明，一般转化为证线面垂直，而线面垂直的证明，往往需多次利用线面垂直判定与性质定理，而线线垂直的证明有时需要利用平几条件，如本题可由余弦定理解出，即

易错点

解题步骤不完整或考虑不全致推理片面导致出错。

第(3)小题正确答案及相关解析

正确答案

（Ⅲ）

解析

试题分析：本题属于立体几何的综合应用问题，属于中档题，只要掌握相关立体几何的定理及性质，即可解决本题，解析如下：

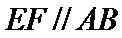
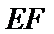
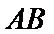
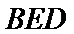
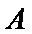
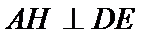
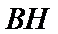
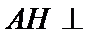
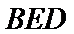
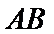
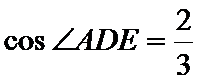
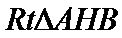
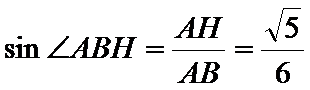
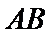
（Ⅲ）解：因为，所以直线与平面所成角即为直线与平面所成角.过点作于点，连接，又因为平面平面，由（Ⅱ）知平面，所以直线与平面所成角即为.在中，，由余弦定理可得，所以，因此，在中，，所以直线与平面所成角的正弦值为

考查方向

本题考查了直线与平面平行和垂直、平面与平面垂直、直线与平面所成角等知识点。

解题思路

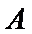
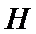
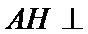
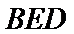
（Ⅲ）求线面角，关键作出射影，即面的垂线，可利用面面垂直的性质定理得到线面垂直，即面的垂线：过点作于点，则平面，从而直线与平面所成角即为.再结合三角形可求得正弦值

易错点

解题步骤不完整或考虑不全致推理片面导致出错。

1

题型：简答题

|

简答题 · 14 分

现需要设计一个仓库，它由上下两部分组成，上部分的形状是正四棱锥，下部分的形状是正四棱柱（如图所示），并要求正四棱柱的高是正四棱锥的高的倍．

19．若，，则仓库的容积是多少；

20．若正四棱锥的侧棱长为，当为多少时，仓库的容积最大？

第(1)小题正确答案及相关解析

正确答案

；

解析

，则，

，，

，

故仓库的容积为；

考查方向

函数的概念、导数的应用、棱柱和棱锥的体积

解题思路

易错点

列函数解析式，求导与分类讨论。

第(2)小题正确答案及相关解析

正确答案

；

解析

设，仓库的容积为

则，，，

，

当时，，单调递增，

当时，，单调递减，

因此，当时，取到最大值，

即时，仓库的容积最大．

考查方向

函数的概念、导数的应用、棱柱和棱锥的体积

解题思路

易错点

列函数解析式，求导与分类讨论。

1

题型：单选题

|

单选题 · 5 分

7．若是两条不同的直线，垂直于平面，则“ ”是“ 的（）

A充分而不必要条件

B必要而不充分条件

C充分必要条件

D既不充分也不必要条件

正确答案

B

解析

若，因为垂直于平面，则或；若，又垂直于平面，则，所以“ ”是“ 的必要不充分条件，故选B．

考查方向

空间直线和平面、直线和直线的位置关系．

解题思路

利用直线与平面平行于垂直的关系，结合充分条件和必要条件性质，判断关系。

易错点

逻辑混乱，直线与平面的位置关系掌握不牢

知识点

充要条件的判定平面与平面平行的判定与性质平面与平面垂直的判定与性质

1

题型：简答题

|

简答题 · 14 分

如图，在直三棱柱中，分别为的中点，点在侧棱上，

且，．

17．直线平面；

18.平面平面．

第(1)小题正确答案及相关解析

正确答案

为中点，为的中位线

又为棱柱，

，又平面，且

平面；

解析

为中点，为的中位线

又为棱柱，

，又平面，且

平面；

考查方向

直线与直线、平面与平面位置关系

解题思路

易错点

判定定理的选用，线面关系的转化

第(2)小题正确答案及相关解析

正确答案

为直棱柱，平面

，又

且，平面

平面，

又，平面

又平面，

又，，且平面

平面，又

平面平面．

解析

为直棱柱，平面

，又

且，平面

平面，

又，平面

又平面，

又，，且平面

平面，又

平面平面．

考查方向

直线与直线、平面与平面位置关系

解题思路

易错点

判定定理的选用，线面关系的转化

1

题型：单选题

|

单选题 · 5 分

10.已知是球的球面上两点,,为该球面上的动点.若三棱锥体积的最大值为36,则球的表面积为（）

A

B

C

D

正确答案

C

解析

设球的半径为R,则△AOB面积为,三棱锥体积最大时,C到平面AOB距离最大且为R,此时 ,所以球O的表面积.故选C.

考查方向

本题考查球的半径与表面积，考查体积的计算，确定点C位于垂直于面AOB的直径端点时，三棱锥O-ABC的体积最大是关键．

解题思路

由于三棱锥底面AOB面积为定值,故高最大时体积最大,本题就是利用此结论求球的半径,然后再求出球的表面积,由于球与几何体的切接问题能很好的考查空间想象能力,使得这类问题一直是高考中的热点及难点,提醒考生要加强此方面的训练.

易错点

截面圆外接圆半径的计算，及取得最值时顶点位置的确定.

知识点

平面与平面平行的判定与性质

1

题型：单选题

|

单选题 · 5 分

4．设是不同的平面，是不同的直线，则由下列条件能得出的是（）

A

B

C

D

正确答案

A

解析

由知，又因为，所以，故本题选择A选项。

考查方向

本题主要考查了空间点线面的位置关系，为高考常考题，在近几年的各省高考题出现的频率较高，常与空间点线面的位置关系、线线、线面、面面平行与垂直的判定定理及性质定理等知识点交汇命题。

解题思路

直接根据相关定理进行判断。

易错点

空间点线面的位置关系、线线、线面、面面平行与垂直的相关定理不熟悉导致出错。

知识点

直线与平面平行的判定与性质平面与平面平行的判定与性质直线与平面垂直的判定与性质平面与平面垂直的判定与性质

1

题型：简答题

|

简答题 · 12 分

19．如图，已知平面，四边形为矩形，四边形为直角梯形，，，，．

（I）求证：平面；

（II）求证：平面；

(Ⅲ)求三棱锥的体积．

正确答案

（1）见解析；（2）见解析；（3）

解析

试题分析：本题属于立体几何中有关线面平行和线面垂直的证明以及求体积的基本问题，

（1）直接利用线面平行的判定定理来证明；

（2）由线线垂直到线面垂直即线面垂直的判定定理；

（3）换底后直接利用体积公式来求解。

考查方向

本题考查了线面平行和线面垂直的证明以及求体积。

解题思路

本题考查立体几何中有关线面平行和线面垂直的证明以及求体积，解题步骤如下：

（1）直接利用线面平行的判定定理来证明；

（2）由线线垂直到线面垂直即线面垂直的判定定理；

（3）换底后直接利用体积公式来求解。

易错点

定理使用条件不全。

知识点

组合几何体的面积、体积问题平面与平面平行的判定与性质平面与平面垂直的判定与性质

1

题型：简答题

|

简答题 · 12 分

19．如图，在矩形ABCD中，AB＝2，AD＝1，M为DC的中点．将△ADM沿AM折起，使得平面ADM⊥平面ABCM．

（Ⅰ）若E为BD的中点，求证：

正确答案

（1）见解析；（2）

解析

试题分析：本题属于立体几何的证明与体积的计算问题，

（1）由已知条件然后结合线面平行的判定定理来证明；

（2）将底面换了之后再来计算其体积。

（1）证明：取的中点，连接，则且

又且，且，四边形是平行四边形

…………(6分)

（2）在平面图形，连接，易证是等腰直角三角形，

，

…………(12分)

考查方向

本题考查了立体几何的证明与体积的计算问题。

解题思路

本题考查立体几何的证明与体积的计算问题，解题步骤如下：

（1）由已知条件然后结合线面平行的判定定理来证明；

（2）将底面换了之后再来计算其体积。

易错点

不会换底去计算体积。

知识点

平面与平面平行的判定与性质直线、平面垂直的综合应用

1

题型：简答题

|

简答题 · 12 分

19．如图所示的多面体中，是菱形，是矩形，面，

（Ⅰ）求证：平面平面；

（Ⅱ）若，求四棱锥的体积．

正确答案

（1）见详解；（2）

解析

试题分析：本题属于立体几何证明与体积的计算问题，

（1）由线线到线面再到面面平行

（2）利用椎体的体积公式求解．

考查方向

本题考查了立体几何．

解题思路

本题考查立体几何证明与体积的计算问题，解题步骤如下：

由线线到线面再到面面平行。

利用椎体的体积公式求解。

易错点

第1问面面平行的判定定理不熟练，条件写的不全，第2问不会求高。

知识点

棱柱、棱锥、棱台的体积平面与平面平行的判定与性质

1

题型：简答题

|

简答题 · 12 分

19. 如图，在三棱锥中，平面90°，E是AB的中点，M是CE的中点，N点在PB上，且.

（I）证明：平面平面PAB；

（II）证明：MN//平面PAC.

正确答案

见解析

解析

考查方向

本题考察了直线和平面平行的判定定理，考察了面和面垂直的判定定理，考察了面与面之间的位置关系，

解题思路

该题解题关键在于找到所求内容的突破点

1）根据平面

2）由线面垂直得到面面垂直

3）取AE的中点，借助中位线由面面平行证明线面平行

易错点

本题容易在辅助线建立过程出错

知识点

平面与平面平行的判定与性质平面与平面垂直的判定与性质

1

题型：简答题

|

简答题 · 12 分

如图，在三棱柱中，是等边三角形，,是中点.

22.求证：平面；

23.当三棱锥体积最大时求点到平面的距离.

第(1)小题正确答案及相关解析

正确答案

(略)

解析

连结，交于，连.在三棱柱中，四边形为平行四边形，则,又是中点，∴，而平面，平面，∴平面.

考查方向

线面平行的位置关系，点到平面的距离，体积桥求距离的应用

解题思路

关键是在面DCB1中找线，连结，交于，可证DO//A1B

易错点

确定“三棱锥体积最大时”的条件

第(2)小题正确答案及相关解析

正确答案

解析

设点到平面的距离是，则，而，故当三棱锥体积最大时，，即平面.

由（Ⅰ）知：，所以到平面的距离与到平面的距离相等.

∵平面，平面，∴，

∵是等边三角形，是中点，∴，又，平面，平面，∴平面，∴，由计算得：，所以，设到平面的距离为，由得：，所以到平面的距离是

考查方向

线面平行的位置关系，点到平面的距离，体积桥求距离的应用

解题思路

当三棱锥体积最大时，，即平面，再利用体积桥即可求得点到平面的距离.

易错点

确定“三棱锥体积最大时”的条件

1

题型：简答题

|

简答题 · 12 分

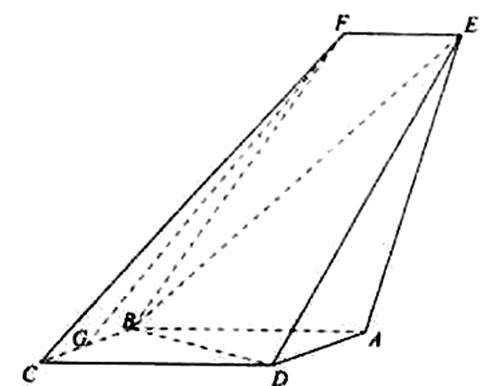
19．如图，空间几何体中，四边形是梯形，四边形是矩形，且平面⊥平面，，，是线段上的动点．

（1）试确定点的位置，使//平面，并说明理由；

（2）在（1）的条件下，平面将几何体分成两部分，求空间几何体与空间几何体的体积之比；

正确答案

（1）M是线段AE的中点，证明见解析；（2）

解析

试题分析：本题属立体几何中的有关证明和体积有关的计算问题，题目的难度是逐渐由易到难，（1）根据线面平行的判定定理来证明；（2）将2个几何体的体积计算出来再计算出比值。

试题解析：（Ⅰ）当M是线段AE的中点时，AC//平面MDF，证明如下： 1

连结CE交DF于N，连结MN，由于M、N分别是AE、CE的中点，

所以MN//AC，又MN在平面MDF内，所以AC//平面MDF （Ⅱ）将几何体ADE－BCF补成三棱柱ADE－，

三棱柱ADE－的体积为△ADE·CD= 则几何体ADE－BCF的体积

10分

又三棱锥F－DEM的体积 ∴ 两几何体的体积之比为：（）=

考查方向

本题考查了立体几何中的有关证明和体积有关的计算问题。

解题思路

本题考查了立体几何中的有关证明和体积有关的计算问题，解题步骤如下：（1）根据线面平行的判定定理来证明；（2）将2个几何体的体积计算出来再计算出比值。

易错点

不会求体积。

知识点

组合几何体的面积、体积问题直线与平面平行的判定与性质平面与平面平行的判定与性质

1

题型：简答题

|

简答题 · 12 分

如图，在三棱柱中，是等边三角形，,是中点.

22.求证：平面；

23.当三棱锥体积最大时求点到平面的距离.

第(1)小题正确答案及相关解析

正确答案

(略)

解析

连结，交于，连.在三棱柱中，四边形为平行四边形，则,又是中点，∴，而平面，平面，∴平面.

考查方向

线面平行的位置关系，点到平面的距离，体积桥求距离的应用

解题思路

关键是在面DCB1中找线，连结，交于，可证DO//A1B

易错点

确定“三棱锥体积最大时”的条件

第(2)小题正确答案及相关解析

正确答案

解析

设点到平面的距离是，则，而，故当三棱锥体积最大时，，即平面.

由（Ⅰ）知：，所以到平面的距离与到平面的距离相等.

∵平面，平面，∴，

∵是等边三角形，是中点，∴，又，平面，平面，∴平面，∴，由计算得：，所以，设到平面的距离为，由得：，所以到平面的距离是

考查方向

线面平行的位置关系，点到平面的距离，体积桥求距离的应用

解题思路

当三棱锥体积最大时，，即平面，再利用体积桥即可求得点到平面的距离.

易错点

确定“三棱锥体积最大时”的条件

热门试卷

正确答案

考查方向

解题思路

易错点

知识点

正确答案

解析

考查方向

解题思路

易错点

知识点

正确答案

解析

考查方向

解题思路

易错点

正确答案

解析

考查方向

解题思路

易错点

正确答案

解析

考查方向

解题思路

易错点

正确答案

解析

考查方向

解题思路

易错点

正确答案

解析

考查方向

解题思路

易错点

正确答案

解析

考查方向

解题思路

易错点

知识点

正确答案

解析

考查方向

解题思路

易错点

正确答案

解析

考查方向

解题思路

易错点

正确答案

解析

考查方向

解题思路

易错点

知识点

正确答案

解析

考查方向

解题思路

易错点

知识点

正确答案

解析

考查方向

解题思路

易错点

知识点

正确答案

解析

考查方向

解题思路

易错点

知识点

正确答案

解析

考查方向