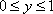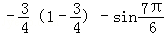- 立体几何与空间向量
- 共2637题
请你谈一谈对“不同生产方式以及生产工艺中,生产物流管理所采用的方法和手段是不同的。”这句话的理解。
正确答案
测试
从字母

正确答案
解析
略
知识点
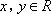
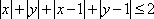
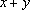
正确答案
解析
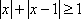
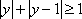

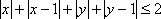
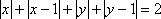
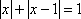
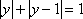

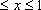

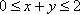
知识点
函数f(x)=
正确答案
解析
由y=f(x)=


∵x>0,∴y>0.
∴f-1(x)=
知识点
若函数f(x)(x∈R)是周期为4的奇函数,且在[0,2]上的解析式为f(x)=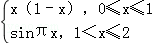
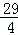
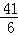
正确答案
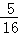
解析
函数f(x)(x∈R)是周期为4的奇函数,且在[0,2]上的解析式为f(x)=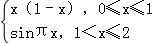
则f(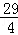
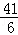
=f(8﹣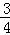
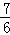
=f(﹣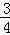
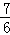
=﹣f(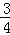
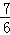
=
=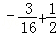
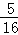
知识点
设F1,F2分别是椭圆E: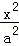
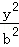
(1)若|AB|=4,△ABF2的周长为16,求|AF2|;
(2)若cos∠AF2B=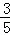
正确答案
(1)|AF2|=5
(2)e=
解析
(1)∵|AB|=4,|AF1|=3|F1B|,
∴|AF1|=3,|F1B|=1,
∵△ABF2的周长为16,
∴4a=16,
∴|AF1|+|AF2|=2a=8,
∴|AF2|=5;
(2)设|F1B|=k(k>0),则|AF1|=3k,|AB|=4k,
∴|AF2|=2a﹣3k,|BF2|=2a﹣k
∵cos∠AF2B=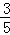
∴(4k)2=(2a﹣3k)2+(2a﹣k)2﹣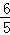
化简可得a=3k,
∴|AF2|=|AF1|=3k,|BF2|=5k
∴|BF2|2=|AF2|2+|AB|2,
∴AF1⊥AF2,
∴△AF1F2是等腰直角三角形,
∴c=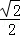
∴e=

知识点
若x,y满足约束条件
正确答案
0
解析
z=-x+y⇒y=x+z,z表示直线y=x+z在y轴上的截距,截距越小,z就越小,画出题中约束条件表示的可行域(如图中阴影部分所示),当直线过点A(1,1)时,zmin=0.
知识点
已知函数


(1)若

(2)若


正确答案
见解析。
解析
(1) 当

∵ 

∴ 


当


(2)
当


当


知识点
已知复数


正确答案
21
解析

知识点
已知向量
正确答案
10
解析
知识点
请你谈一谈对“不同生产方式以及生产工艺中,生产物流管理所采用的方法和手段是不同的。”这句话的理解。
正确答案
测试
某保险公司利用简单随机抽样方法,对投保车辆进行抽样,样本车辆中每辆车的赔付结果统计如下:
(1)若每辆车的投保金额均为2800元,估计赔付金额大于投保金额的概率;
(2)在样本车辆中,车主是新司机的占10%,在赔付金额为4000元的样本车辆中,车主是新司机的占20%,估计在已投保车辆中,新司机获赔金额为4000元的概率。
正确答案
(1)0.27
(2)0.24
解析
(1)设A表示事件“赔付金额为3000元,”B表示事件“赔付金额为4000元”,以频率估计概率得
P(A)=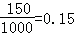
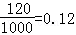
由于投保额为2800元,赔付金额大于投保金额得情形是3000元和4000元,所以其概率为P(A)+P(B)=0.15+0.12=0.27。
(2)设C表示事件“投保车辆中新司机获赔4000元”,由已知,样本车辆中车主为新司机的有0.1×1000=100,而赔付金额为4000元的车辆中车主为新司机的有0.2×120=24,
所以样本中车辆中新司机车主获赔金额为4000元的频率为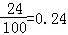
由频率估计概率得P(C)=0.24。
知识点
设复数z满足(z﹣2i)(2﹣i)=5,则z=( )
正确答案
解析
由(z﹣2i)(2﹣i)=5,得:

∴z=2+3i。
知识点
有一个容量为66的样本,数据的分组及各组的频数如下:
[11.5,15.5) 2 [15.5,19.5) 4 [19.5,23.5) 9 [23.5,27.5) 18
[27.5,31.5) 1l [31.5,35.5) 12 [35.5,39.5) 7 [39.5,43.5) 3
根据样本的频率分布估计,大于或等于31.5的数据约占
正确答案
解析
大于或等于31.5的数据共有12+7+3=22个,约占
知识点
设a,b,m,n∈R,且a2+b2=5,ma+nb=5,则
正确答案
解析
由柯西不等式得,
(ma+nb)2≤(m2+n2)(a2+b2)
∵a2+b2=5,ma+nb=5,
∴(m2+n2)≥5
∴
故答案为:
知识点
扫码查看完整答案与解析