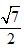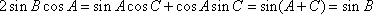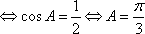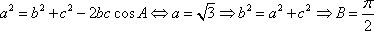- 立体几何与空间向量
- 共2637题
请你谈一谈对“不同生产方式以及生产工艺中，生产物流管理所采用的方法和手段是不同的。”这句话的理解。
正确答案
测试
请你谈一谈对“不同生产方式以及生产工艺中，生产物流管理所采用的方法和手段是不同的。”这句话的理解。
正确答案
测试
设等差数列{an}的公差为d，点(an，bn)在函数f(x)＝2x的图象上(n∈N*)。
(1)证明：数列{bn}为等比数列；
(2)若a1＝1，函数f(x)的图象在点(a2，b2)处的切线在x轴上的截距为
正确答案
见解析
解析
(1)证明：由已知，bn＝
当n≥1时，
所以，数列{bn}是首项为
(2)函数f(x)＝2x在(a2，b2)处的切线方程为y－
它在x轴上的截距为
由题意，
解得a2＝2.
所以，d＝a2－a1＝1，an＝n，bn＝2n，
于是，Tn＝1×4＋2×42＋3×43＋…＋(n－1)·4n－1＋n·4n，
4Tn＝1×42＋2×43＋…＋(n－1)×4n＋n·4n＋1.
因此，Tn－4Tn＝4＋42＋…＋4n－n·4n＋1
所以，
知识点
如图，长方体
（1）证明：
（2）如果
正确答案
见解析
解析
（I）连接
长方体
（2）在矩形
得：
知识点
设
A
B
C
D
正确答案
解析
化简
因为
知识点
已知点A（﹣2，3）在抛物线C：y2=2px的准线上，记C的焦点为F，则直线AF的斜率为（ ）
A﹣
B﹣1
C﹣
D﹣
正确答案
解析
∵点A（﹣2，3）在抛物线C：y2=2px的准线上，
∴
∴F（2，0），
∴直线AF的斜率为
知识点
已知m，n表示两条不同直线，α表示平面，下列说法正确的是（ ）
正确答案
解析
A)若m∥α，n∥α，则m，n相交或平行或异面，故A错；
B)若m⊥α，n⊂α，则m⊥n，故B正确；
C)若m⊥α，m⊥n，则n∥α或n⊂α，故C错；
D)若m∥α，m⊥n，则n∥α或n⊂α或n⊥α，故D错。
知识点
设等差数列{an}的公差为d，若数列{2
正确答案
解析
∵数列{2
∴
∴
∴a1（an+1﹣an）=a1d＜0
知识点
设△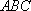
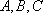
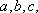
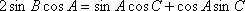
（1）求角A的大小；
（2）若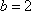
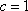
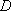
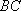
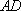
正确答案
（1）
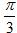
解析
（1）
（II）
在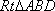
知识点
某几何体的三视图如图所示，则它的体积是（ ）
A
B
C8-2π
D
正确答案
解析
选A 由几何体的三视图可知几何体为一个组合体，
即一个正方体中间去掉一个圆锥体，所以它的体积是
知识点
函数f(x)＝xcos2x在区间[0,2π]上的零点的个数为( )
正确答案
解析
令f(x)＝xcos2x＝0，得x＝0或cos2x＝0，故x＝0或2x＝kπ＋
知识点
若函数
A
B
C3
D4
正确答案
解析
∵
当且仅当
知识点
如图，正方体ABCD-A1B1C1D1中，AB=2。，点E为AD的中点，点F在CD上，若EF∥平面AB1C，则线段EF的长度等于________。
正确答案
解析
由EF∥平面AB1C可得
EF=
知识点
已知向量
A
B
C6
D12
正确答案
解析
略
知识点
如题（20）图，在四面体
（1）求四面体ABCD的体积；
（2）求二面角C-AB-D的平面角的正切值.
正确答案
（1） 
解析
（1）如答（20）图1，过D作DF⊥AC垂足为F，
故由平面ABC⊥平面ACD，知DF⊥平面ABC，即DF
是四面体ABCD的面ABC上的高，设G为边CD的中点，
则由AC=AD，知AG⊥CD，从而
由
故四面体ABCD的体积
（2）如答（20）图1，过F作FE⊥AB，垂足为E，连接DE.
由（1）知DF⊥平面ABC.
由三垂线定理知DE⊥AB，故∠DEF为二面角C—AB—D的平面角.
在
在
在Rt△DEF中，
知识点
扫码查看完整答案与解析