- 立体几何与空间向量
- 共2637题
已知锐角


正确答案
解析
略
知识点

正确答案
解析
略
知识点
如图,平行四边形ABCD中,

正确答案
解析
略
知识点
某学校对1 000名高三毕业学生的体育水平测试成绩进行统计,得到样本频率分布直方图如图所示,现规定不低于70分为合格,则合格人数是______。
正确答案
600
解析
不低于70分的人数的频率为

知识点
如图,在三棱柱







(1) 证明:

(2)证明:平面

正确答案
见解析。
解析
知识点
一个四棱锥的底面为正方形,其三视图如图所示,则这个四棱锥的体积是
正确答案
解析
略
知识点
将长方体截去一个四棱锥,得到的几何体如图所示,则该几何体的左视图( )
正确答案
解析
根据三视图的特点,知道左视图从图形的左边向右边看,看到一个正方形的面,在面上有一条对角线,对角线是由左下角都右上角的线,得到结果。
解:左视图从图形的左边向右边看,
看到一个正方形的面,
在面上有一条对角线,
对角线是由左下角都右上角的线,
故选D。
知识点
一圆形纸片的圆心为点









正确答案
解析
略
知识点
如图4,在四棱锥







(1)求证:

(2)求证:
(3)若


正确答案
见解析。
解析
(1)证明:连接




∵
∴

∵

∴
∵



∴

(2)证明:∵



∴
∵

∴

∴
∴
∵




∴

∵

∴
(3)解:取




∵


∴


在Rt△


∵

∴
在Rt△

在△



∴
在Rt△

在Rt△

∴
设点


∵
∴
即

∴点

知识点
一个三棱锥的三视图是三个直角三角形,如图所示,则该三棱锥的外接球的表面积为( )
正确答案
解析
由三视图复原几何体,几何体是底面是直角三角形,
一条侧棱垂直底面直角顶点的三棱锥;把它扩展为长方体,两者有相同的外接球,
它的对角线的长为球的直径:

该三棱锥的外接球的表面积为:
故选A。
知识点
如图,直四棱柱




(1)求证:

(2)求证:平面

正确答案
见解析
解析
(1)连接


由已知四边形


又



所以
因为



所以

(2)由已知
又



∴
∵


∵底面



∴
又



∴

∵
∴平面

知识点
已知双曲线与椭圆

正确答案
解析
略
知识点
四面体的四个面的面积分别为





正确答案
解析
略
知识点
定义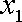
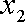
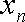
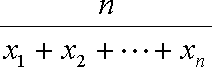
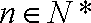
(1)若数列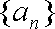
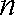
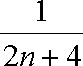
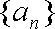
(2)设数列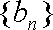
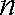
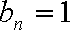
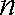
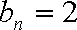
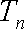
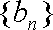
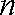
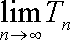
(3)设函数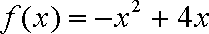
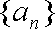
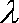

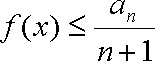
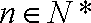
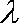
正确答案
见解析
解析
(1)设数列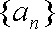
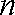
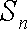
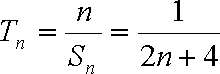
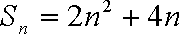
所以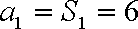

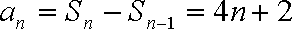
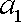
所以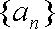
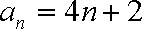
(2)设数列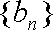
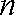
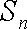
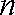
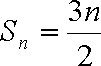
当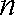
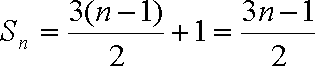
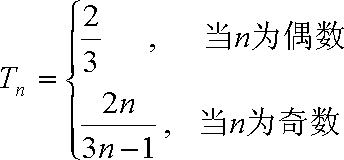
所以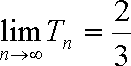
(3)假设存在实数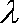

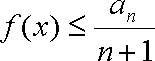
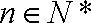
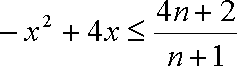
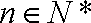
令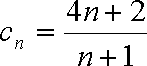
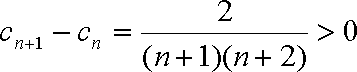
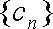
所以只要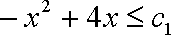
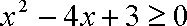


所以存在最大的实数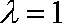

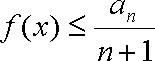
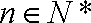
知识点
如图所示的几何体,是由棱长为2的正方体
(1)试画出该几何体的三视图;(主视图投影面平行平面
(2)若截面

正确答案
见解析
解析
(1) (每画对一个图形得2分)

(2)设原正方体中由顶点

结合题意,可知,



知识点
扫码查看完整答案与解析





















































