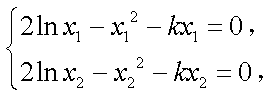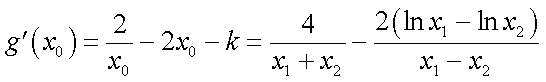- 立体几何与空间向量
- 共2637题
如图,在三棱锥




(1)求证:

(2)若平面



正确答案
见解析。
解析
(1)在





又



所以

(2)在平面



因为平面







又


又







又


知识点
如图,在三棱锥P—ABC中,平面PAC


求证:(1)
(2)平面DEF
正确答案
见解析。
解析
(1)在△PAC中,因为E,F分别是AP,
AC的中点,所以EF // PC。
又因为

所以
(2)连结CD,因为

因为F是AC的中点,所以
因为平面PAC 



所以
因为

知识点
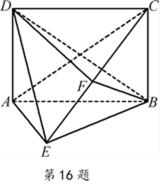
如图,在四棱锥E—ABCD中,底面ABCD为矩形,平面ABCD⊥平面ABE,∠AEB=90°,BE=BC,F为CE的中点,求证:
(1) AE∥平面BDF;
(2) 平面BDF⊥平面BCE。
正确答案
见解析
解析
证明(1) 设AC∩BD=G,连结FG,易知G是AC的中点,
因为 F是EC中点,所以 在△ACE中,FG∥AE
因为 AE⊄平面BDF,FG⊂平面BDF,
所以 AE∥平面BDF。
(2) 因为 平面ABCD⊥平面ABE,BC⊥AB,
平面ABCD∩平面ABE=AB,所以 BC⊥平面ABE,
因为 AE⊂平面ABE,所以 BC⊥AE,
又AE⊥BE,BC∩BE=B,所以 AE⊥平面BCE,又FG∥AE,
所以FG⊥平面BCE,
因为 FG⊂平面BDF,所以平面BDF⊥平面BCE
知识点
如图是某直三棱柱(侧棱与底面垂直)被削去上底后的直观图与三视图的侧视图、俯视图,在直观图中,

(1)求出该几何体的体积。
(2)若



(3)求证:平面

正确答案
见解析。
解析
(1)由题意可知:四棱锥
平面

所以,

又
则四棱锥

(2)连接
又






所以,

(3)


又平面


由(2)知:

又
所以,平面

知识点
若一个底面是正三角形的三棱锥的俯视图如图所示,则其主视图与侧视图面积之比等于
正确答案
解析
设正三角形的边长


知识点
如图所示,PA⊥平面ABCD,四边形ABCD为正方形,且2PA=AD, E、F、G、H分别是线段PA、PD、CD、BC的中点.
(1)求证:BC∥平面EFG;
(2)求证:DH⊥平面AEG;
(3)求三棱锥E-AFG与四棱锥P-ABCD的体积比.
正确答案
见解析。
解析
(1)∵BC∥AD,AD∥EF,∴BC∥EF,,,,,,,,,。2分

(2)∵PA⊥平面ABCD,∴PA⊥DH ,即 AE⊥DH,,,,,,,,,。5分
∵△ADG≌△DCH ,∴∠HDC=∠DAG,∠AGD+∠DAG=90°
∴∠AGD+∠HDC=90°
∴DH⊥AG
又∵AE∩AG=A,∴DH⊥平面AEG,,,,,,,,,,,。8分
(3)

知识点
已知四棱柱




正确答案
解析
由条件可得,A、M、P、N四点在以PA为直径的圆上,所以由正弦定理得






知识点
如图,某测量人员,为了测量西江北岸不能到达的两点A,B之间的距离,她在西江南岸找到一个点C,从C点可以观察到点A,B;找到一个点D,从D点可以观察到点A,C;到一个点E,从E点可以观察到点B,C;并测量得到数据:∠ACD=90°,∠ADC= 60°,∠ACB =15°,∠BCE =105°,∠CEB =45°,DC=CE =1(百米)。
(1)求△CDE的面积;
(2)求A,B之间的距离。
正确答案
(1)

解析
(1)连结DE,在CDE中,

(2)依题意知,在RTACD中,
在BCE中,
由正弦定理
得
∵

在ABC中,由余弦定理
可得
∴
知识点
已知正实数x,y满足xy+2x+y=4,则x+y的最小值为 
正确答案
解析
∵正实数x,y满足xy+2x+y=4,
∴
∴x+y=x+




当且仅当x=
∴x+y的最小值为
知识点
设函数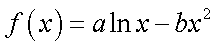
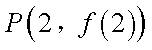
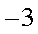
(1)求函数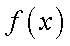
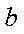
(2)当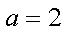
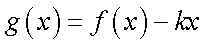
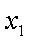
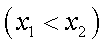
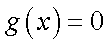
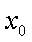
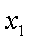
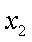
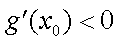
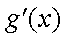
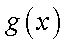
正确答案
见解析。
解析
(1)函数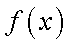
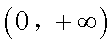
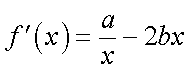
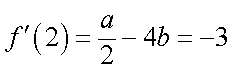
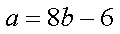
于是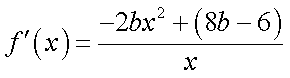
①当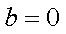
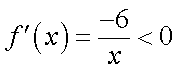
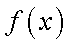
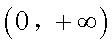
②当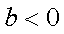
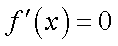
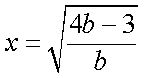
所以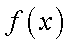
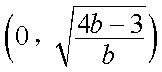
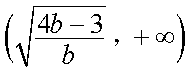
③当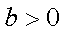
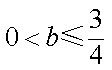
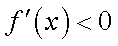
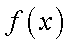
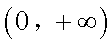
若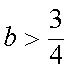
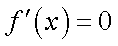
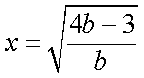
所以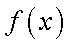
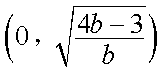
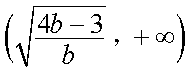
综上,若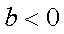
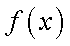
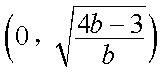
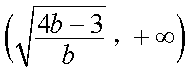
若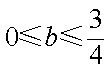
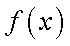
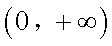
若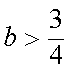
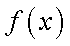
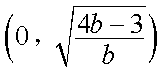
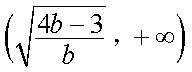
(2)因为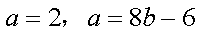
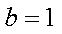
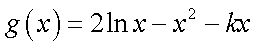
因为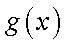
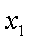
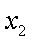
相减得: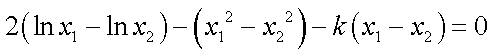
因为 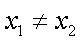
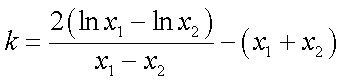
于是
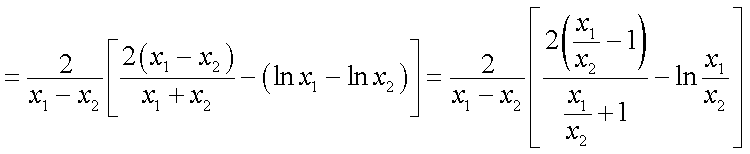
令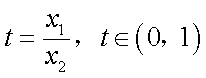
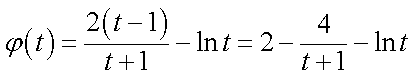
则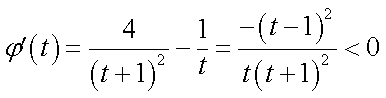
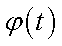
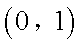
则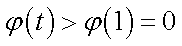
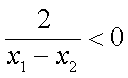
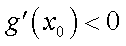
知识点
如图,AB为圆O的直径,点E,F在圆上,四边形ABCD为矩形,AB∥EF,∠BAF=
(1)BF⊥平面DAF;
(2)ME∥平面DAF。
正确答案
见解析。
解析
(1)因四边形ABCD为矩形,
故DA⊥AB。
因平面ABCD⊥平面ABEF,且DA⊂平面ABCD,平面ABCD∩平面ABEF=AB,
故DA⊥平面ABEF
因BF⊂平面ABEF,
故DA⊥BF
因AB为直径,
故BF⊥AF。
因DA,AF为平面DAF内的两条相交直线,
故BF⊥平面DAF
(2)因∠BAF=
故EF=
取DA中点N,连NF,MN,
因M为BD的中点,
故MN∥AB,且MN=
于是四边形MNFE为平行四边形,
所以ME∥NF
因NF⊂平面DAF,ME⊄平面DAF,
故ME∥平面DAF
知识点
已知正六棱锥的底面边长是3,侧棱长为5,则该正六棱锥的体积是 。
正确答案
解析
若正六棱锥的底面边长为3
则其底面积S=6×(

又∵正六棱锥的侧棱长为5
故棱锥的高为
故正六棱锥的体积V=
知识点
如图,在三棱柱




(1)求证:AB⊥平面AA1 C1C;
(2)若线段




(3)证明:
正确答案
见解析
解析
(1)






(2)














(3)




由(1)可得




又




知识点
已知A(

(1)求动点P的轨迹方程;
(2)设直线
正确答案
见解析。
解析
(1)∵|PA|+|PB|=2>
∴点P的轨迹是以A,B为焦点,长轴长2a=2的椭圆,…………………………………………2分
∴a=1, 
设P(x,y),∴点P的轨迹方程为
(2)将

消去x,整理为
设
则
=
当且仅当

此时直线l的方程是
知识点
如图,在四棱锥P—ABCD中,底面ABCD是正方形,侧棱PD⊥底面ABCD,PD=DC,E是PC的中点,作EF⊥PB交PB于点F。
(1)证明PA//平面EDB;
(2)证明PB⊥平面EFD;
正确答案
见解析。
解析
(1)
证明:连结AC,AC交BD于O,连结EO。
∵底面ABCD是正方形,∴点O是AC的中点
在
而

所以,PA // 平面EDB…………………………6分
(2)证明:
∵PD⊥底面ABCD且
∴
∵PD=DC,可知
∴
同理由PD⊥底面ABCD,得PD⊥BC。
∵底面ABCD是正方形,有DC⊥BC,∴BC⊥平面PDC。
而

由①和②推得
而
又∵EF⊥PB,
知识点
扫码查看完整答案与解析