- 立体几何与空间向量
- 共2637题
如图,已知正方体ABCD—A1B1C1D1,过BD1的平面分别交棱AA1和棱CC1于E、F两点。
(1)求证:A1E=CF;
(2)若E、F分别是棱AA1和棱CC1的中点,求证:平面
正确答案
见解析。
解析
(1)由题知,平面EBFD1与平面BCC1B1交于
BF、与平面ADD1A交于ED1 ………………1分
又平面BCC1B1//平面ADD1A1∴D1E//BF …………………2分
同理BE//D1F ……………………………3分
∴四边形EBFD1为平行四边形 ∴D1E=BF …………………4分
∵A1D1==CB,D1E=BF,∠D1A1E=∠BCF=90°
∴
(2)∵四边形EBFD1是平行四边形。AE=A1E,FC=FC1,
∴Rt△EAB≌Rt△FCB,∴BE=BF,故四边形EBFD1为菱形。 ………………8分
连结
在正方体ABCD—A1B1C1D1中,有B1D1⊥A1C1,B1D⊥A1A
∴B1D1⊥平面A1ACC1。 ………………10分
又EF
又EF
知识点
在直三棱柱

的中点。
(1)证明:平面

(2)证明:
(3)设P是BE的中点,求三棱锥
正确答案
见解析
解析
(1)证明:在
∴

由已知
又∵
(2)证明:取AC的中点M,连结
在
而
在矩形
而
又∵
故
(3)取




由(1)

∵P是BE的中点,
∴
知识点
如图,已知三棱锥P=ABC中,PA⊥PC,D为AB的中点,M为PB的中点,且AB=2PD.
(1)求证:DM//面PAC;
(2)找出三棱锥P—ABC中一组面与面垂直的位置关系,并给出证明(只需找到一组即可).
正确答案
见解析。
解析
(1)证明:依题意D为AB的中点,M为PB的中点

又




(2)平面

证明:由已知
所以PD=BD,又知M为PB的中点

由(1)知

又由已知
故





知识点
如图,在四棱锥





(1)求证:
(2)若平面

求四棱锥
正确答案
见解析。
解析
(1)

又


所以
(2)连接





又


又

又

V
知识点
若

正确答案
解析
略
知识点
在正方体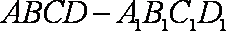
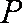
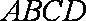
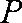
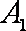
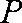
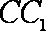
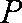
正确答案
解析
略
知识点
如图,四边形


(1)求证:
(2)求证:平面
(3)求体积

正确答案
见解析。
解析
(1)
设BD交AC于M,连结ME.
∵ABCD为正方形,所以M为AC中点,
又∵E为

∴
∴
(2)∵ABCD为正方形 ∴
∵
又
∵
∴
(3)
知识点
已知全集


正确答案
解析
略
知识点
如图,在五面体






(1)证明:
(2)若点





(3)已知空间中有一点O到

正确答案
见解析
解析
解析:
(1)证明:因为
所以 

又因为 
所以 
因为平面





所以 

因为 

所以 
(2)证明:如图,过点





因为 

因为 
所以 
又因为 
所以 


所以四边形
所以 

又因为



所以 

(3)解:点

知识点
如图,在直三棱柱








(1)求证:
(2)求点

正确答案
见解析。
解析
(1)连接

∵





∴



∴



∴

(2)因为
所以


在

∴
知识点
在△ABC中,内角A,B,C,的对边分别为a,b.c
(1)求角A的大小;
(2) 若a=
正确答案
见解析
解析
解:
(1) 由





(2) 由



得

知识点
已知函数f(x)=ax2-ln x,x∈(0,e],其中e是自然对数的底数,a∈R.
(1)当a=1时,求函数f(x)的单调区间与极值;
(2)是否存在实数a,使f(x)的最小值是3?若存在,求出a的值;若不存在,说明理由。
正确答案
见解析
解析
(1)∵f(x)=x2-ln x,f′(x)=2x-=,x∈(0,e],
令f′(x)>0,得<x<e,f′(x)<0,得0<x<,
∴f(x)的单调增区间是,单调减区间为.
∴f(x)的极小值为f=-ln=+ln 2.无极大值, …… 4分
(2)假设存在实数a,使f(x)=ax2-ln x,x∈(0,e]有最小值3,f′(x)=2ax-=。
①当a≤0时,x∈(0,e],所以f′(x)<0,所以f(x)在(0,e]上单调递减,
∴f(x)min=f(e)=ae2-1=3,a=(舍去)。
②当a>0时,令f′(x)=0,得x= ,(ⅰ)当0< <e,即a>时,
f(x)在上单调递减,在上单调递增
∴f(x)min=f=-ln=3,得a=。
(ⅱ)当≥e,即0<a≤时,x∈(0,e]时,f′(x)<0,所以f(x)在(0,e]上单调递减,∴f(x)min=f(e)=ae2-1=3,a=(舍去),此时f(x)无最小值。
综上,存在实数a=,使得当x∈(0,e]时,f(x)有最小值3. …… 14分
知识点
在如图所示的多面体






(1)求证:
(2)求多面体
正确答案
见解析。
解析
(1)
又因平面







(2)作



又



又



故多面体

知识点
7.若偶函数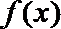
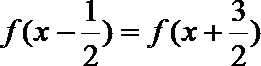
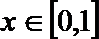
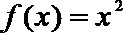
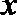
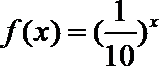
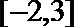
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
1.已知集合


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
扫码查看完整答案与解析


















































































