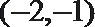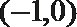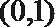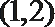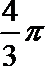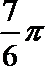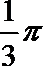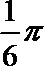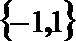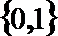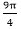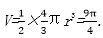- 立体几何与空间向量
- 共2637题
2． 若
正确答案
-1
解析
解析已在路上飞奔，马上就到！
知识点
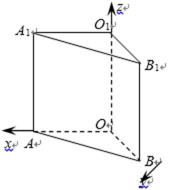
8．如图，直三棱柱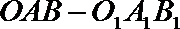
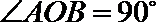
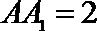
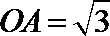
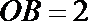
正确答案
解析
解析已在路上飞奔，马上就到！
知识点
6．函数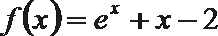
A
B
C
D
正确答案
解析
解析已在路上飞奔，马上就到！
知识点
12．盒中装有形状、大小完全相同的5个小球，其中红色球3个，黄色球2个，若从中随机取出2个球，则取出的2个球颜色不同的概率为_________．
正确答案
解析
解析已在路上飞奔，马上就到！
知识点
20．如图四棱锥
（1）求证：
（2）试在线段
正确答案
解：（1）证明：
（2）设
在平面
则
则四边形
设
则
解析
解析已在路上飞奔，马上就到！
知识点
5．圆锥的侧面展开图为扇形，若其弧长为
正确答案
解析
解析已在路上飞奔，马上就到！
知识点
13．设
正确答案
解析
解析已在路上飞奔，马上就到！
知识点
9．已知棱长为3的正方体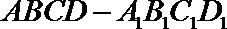
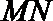
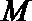
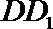
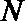
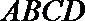
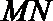
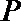
A
B
C
D
正确答案
解析
解析已在路上飞奔，马上就到！
知识点
18．在如图所示的多面体中,四边形
（1）求证：
（2）若
正确答案
解析
解析已在路上飞奔，马上就到！
知识点
1.已知集合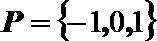
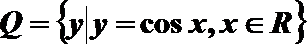
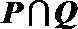
AP
BQ
C
D
正确答案
解析
解析已在路上飞奔，马上就到！
知识点
9.已知四棱锥P-ABCD的底面是正方形，侧棱PA⊥底面ABCD，底面对角线长AC=2，侧面PAB的面积为
正确答案
解析
设底面边长为a，依题意得a2=2， 
知识点
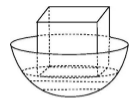
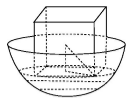
8.如图,有一个水平放置的半球形容器，内有高度为1的溶液，现将一个棱长为2的正方体放入其中，恰好能使液面和正方体的底面完全接触，则该半球形容器的容积为________
正确答案
解析
作出如图所示辅助线，设半球的半径为r,则有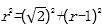
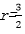
知识点
12.已知
正确答案
60°
解析
解析已在路上飞奔，马上就到！
知识点
12．空间直角坐标系O—xyz中，球心坐标为（-2，0，3），半径为4的球面方程是___________。
正确答案
解析
解析已在路上飞奔，马上就到！
知识点
10．已知三棱锥
A
B
C
D
正确答案
解析
设底面
考查方向
解题思路
先由题中条件求出球的半径，再由球的表面积公式求表面积。
易错点
无法找到球与椎体的联系。
知识点
扫码查看完整答案与解析