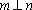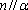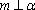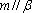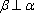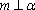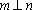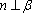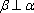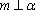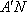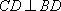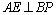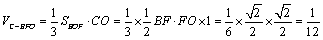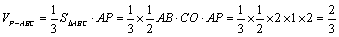- 立体几何与空间向量
- 共2637题
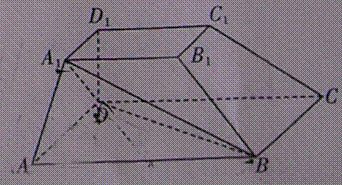
设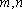
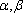
正确答案
解析
对A,若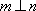
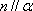

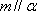
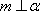
对B,若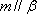
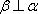

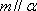

对C,若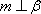
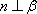
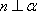
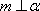
对D,若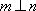
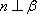
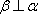
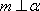

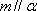
故选C. 点评:本题考查空间中的线线、线面、面面的闻之关系,容易题
知识点
如图,在四棱锥P-ABCD中,AB∥CD,AB⊥AD,CD=2AB,平面PAD⊥平面ABCD,PA⊥AD.E和F分别是CD和PC的中点。
求证:
(1)PA⊥底面ABCD;
(2)BE∥平面PAD;
(3)平面BEF⊥平面PCD.
正确答案
见解析
解析
(1)因为平面PAD⊥底面ABCD,且PA垂直于这两个平面的交线AD,
所以PA⊥底面ABCD.
(2)因为AB∥CD,CD=2AB,E为CD的中点,
所以AB∥DE,且AB=DE.
所以ABED为平行四边形。
所以BE∥AD.
又因为BE

所以BE∥平面PAD.
(3)因为AB⊥AD,而且ABED为平行四边形,
所以BE⊥CD,AD⊥CD.
由(1)知PA⊥底面ABCD,所以PA⊥CD.
所以CD⊥平面PAD.所以CD⊥PD.
因为E和F分别是CD和PC的中点,
所以PD∥EF.所以CD⊥EF.
所以CD⊥平面BEF.
所以平面BEF⊥平面PCD.
知识点
如图,在四棱锥





(1)求证:

(2)求证:

平面


正确答案
见解析
解析
(1)证明:因为底面

又因为 





(2)证明:因为 

又因为 




又因为 


(3)解:如图,连接BD交NC于点F,在平面SNC中过F作

因为 



又因为 



在矩形




所以



知识点
如图,四棱锥



(1)证明:
(2)若


正确答案
见解析
解析
(1)证明:连接


又
而



(2) 由(1)

知识点
如图,四棱锥





(1)证明:
(2)求AB与平面SBC所成角的大小。
正确答案
见解析。
解析
解法一:(1)
取







又

所以
由








所以

另解:由已知易求得






(2)由



作



作


连结

又




作







由于






设




解法二:以



设


又设

(1)

由

故
由

又由

即

于是

故

所以

(2)设平面

则
又
故
取


故


知识点
已知点P,A,B,C,D是球O表面上的点,PA⊥平面ABCD,四边形ABCD是边长为

正确答案
解析
如图所示,∵PA⊥平面ABCD,
∴PA⊥AC。
故可知PC为球O直径,则PC的中点为O,取AC的中点为O′,
则
又∵

∴
∴球半径


∴△OAB为等边三角形。
∴
知识点
设m,n是两条不同的直线,α,β是两个不同的平面( )。
正确答案
解析
A选项中直线m,n可能平行,也可能相交或异面,直线m,n的关系是任意的;B选项中,α与β也可能相交,此时直线m平行于α,β的交线;D选项中,m也可能平行于β.故选C
知识点
如图,在四棱台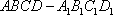
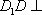
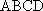
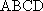
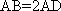
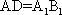
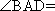
(1)证明: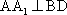
(2)证明: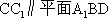
正确答案
见解析。
解析
(1)证明:因为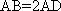
AD=a,则AB=2a,又因为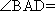
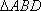
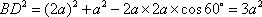
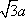

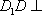
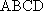


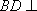
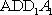
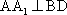
(2)连结AC,设AC
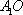
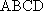
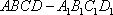
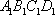
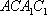
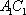
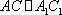
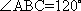
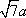
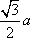
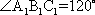
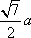
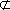


知识点
已知




正确答案
解析
略
知识点
如图,在底面是菱形的四棱锥





(1)求证:

(2)求证:平面

(3)求二面角
正确答案
见解析。
解析
(1)连接BD,交AC于点O,连接OE,在三角形BDP中,







(2)


又








(3)过点



由(2)知,







易得:
知识点
在直角梯形ABCD中,ADBC,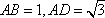
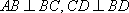
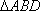
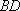
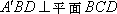
(1)求证: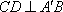
(2)求三棱锥
(3)在线段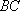
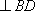
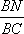
正确答案
见解析。
解析
(1)∵平面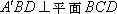
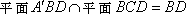
∴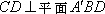
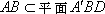
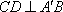
(2)如图(1)在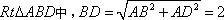
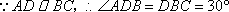
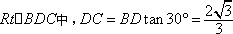
∴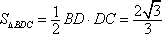
如图(2),在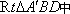
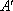

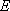
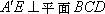
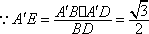
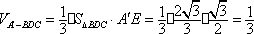
(3)在线段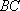
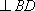
如图(2)在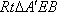
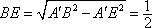
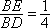
过点E做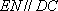
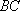
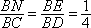
∵
又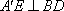
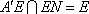
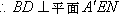
又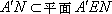
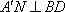
∴在线段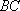
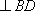
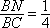
知识点
如图,四棱锥



(1)求证:
(2)求异面直线

正确答案
见解析
解析
(1)∵

∴CD⊥SD
又四边形ABCD是正方形,∴CD⊥AD
∴CD⊥平面SDA

∴SA⊥CD.
(2)∵
∴


由(1),BA⊥平面SDA,∴△SAB是直角三角形.

故异面直线SB与CD所成角的大小为
知识点
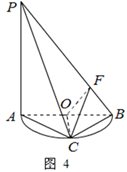
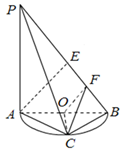
图4,PA垂直于⊙O所在平面ABC,AB为⊙O的直径,PA=AB=2,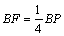
(1)证明:BC平面PAC;
(2)证明:CFBP;
(3)求四棱锥C—AOFP的体积.
正确答案
见解析。
解析
(1)
证明:∵PA⊥平面ABC,BC⊥平面ABC,
∴BC⊥PA.
∵△ACB是直径所对的圆周角,
∴
又∵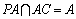
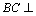
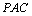
(2)证明:∵PA⊥平面ABC,OC⊥平面ABC,
∴OC⊥PA.
∵C是弧AB的中点,
∴△ABC是等腰三角形,AC=BC,
又O是AB的中点,∴OC⊥AB.
又∵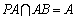
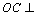
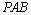
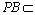
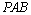
∴
设BP的中点为E,连结AE,则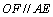
∴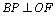
∵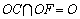
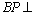
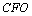
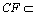
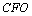
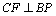
(3)解:由(2)知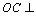
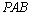
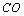

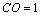
又∵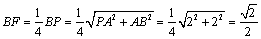
∴
又∵
∴四棱锥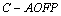
知识点
给定空间中的直线l及平面
正确答案
解析
略
知识点
设m,n是平面


正确答案
解析
略
知识点
扫码查看完整答案与解析