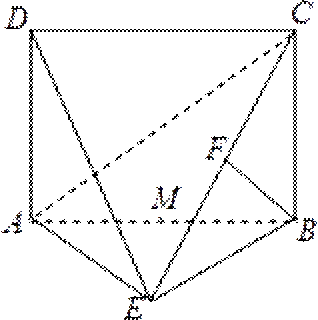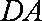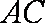- 立体几何与空间向量
- 共2637题
如图,四棱锥P-ABCD中, BC∥AD,BC=1,AD=3,AC⊥CD,且平面PCD⊥平面ABCD.
(1)求证:AC⊥PD;
(2)在线段PA上,是否存在点E,使BE∥平面PCD?若存在,求
正确答案
见解析
解析
(1)∵平面PCD⊥平面ABCD,平面PCD∩平面ABCD=CD, AC⊥CD , AC⊂平面ABCD ,
∴AC⊥平面PCD, ...........................4分
∵PD⊂平面PCD ,
∴AC⊥PD. .................................6分
(2)线段PA上,存在点E,使BE∥平面PCD, ......7分
∵AD=3,
∴在△PAD中,存在EF//AD(E,F分别在AP,PD上),且使EF=1,
又∵ BC∥AD,∴BC∥EF,且BC=EF,
∴四边形BCFE是平行四边形, ...............................9分
∴BE//CF, 
∴BE∥平面PCD, .......................................11分
∵EF =1,AD=3,
∴
知识点
在四棱锥








(1)求证:PA//平面BEF;
(2)求证:
正确答案
见解析
解析
(1)证明:连接AC交BE于O,并连接EC,FO









又







(2)连接




知识点
已知:正方体


(1)求证:
(2)求证:

(3)求三棱锥
正确答案
见解析。
解析
(1)
证明:连结


∵




又


∵


∴
(2)证明:
作

∵


∴四边形

∵


又

∴四边形


∵

∴平面

又



(3)

知识点
如图,已知






(1)求

(2)求

正确答案
见解析
解析
(1)








在

所以
即


(2)






知识点
如图,在四棱锥












(1)若



(2)求证:平面

(3)是否存在点


写出证明过程并求出线段
正确答案
见解析
解析
(1)因为

所以 
因为

而



所以

(2)因为平面

平面




所以




又因为



而

所以平面

(3)存在点


在棱


由已知,



由平面几何知识可得 
由(2)知,


因为


而


又因为


在

可求得,
可见直线



知识点
已知ABC是边长为3的等边三角形,点D、E分别是边AB、AC上的点,且满足==.将ADE沿DE折起到1ADE的位置,并使得平面A1DE⊥平面BCED.
(1)求证:A1D⊥EC;
(2)求三棱锥E-A1CD的高。
正确答案
见解析
解析
解析:(1)因为等边△

所以



由余弦定理得
因为
所以
折叠

因为平面







故A1D⊥EC.…………6分
(2)法一:由(2)的证明,可知


以
















所以


所以
因为







所以
①若


②若
令
因为函数

即
所以
故所求的最大值为
法二:如图,作



由(1)有



所以


所以






所以A1H=
所以在


①若x=0,则tan


②若

令
因为函数

所以tan

知识点
如图,四棱锥P—ABCD中,PD⊥平面ABCD,底面ABCD为矩形,PD=DC=4,AD=2,E为PC的中点.
(1)求证:AD⊥PC;
(2)求三棱锥P-ADE的体积;
(3)在线段AC上是否存在一点M,使得PA//平面EDM,若存在,求出AM的长;若不存在,请说明理由.
正确答案
见解析。
解析
(1)证明:因为PD⊥平面ABCD.
所以PD⊥AD.
又因为ABCD是矩形,
所以AD⊥CD.…………………………………………………………………2分
因为
所以AD⊥平面PCD.
又因为
所以AD⊥PC.………………………………4分
(2)解:因为AD⊥平面PCD,VP-ADE=VA-PDE,…………………………………6分
所以AD是三棱锥A—PDE的高.
因为E为PC的中点,且PD=DC=4,
所以
又AD=2,
所以
(3)
取AC中点M,连结EM、DM,
因为E为PC的中点,M是AC的中点,
所以EM//PA,
又因为EM

所以PA//平面EDM.…………………………………………………………10分
所以
即在AC边上存在一点M,使得PA//平面EDM,AM的长为
知识点
如图,四边形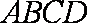
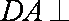
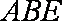
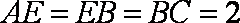
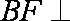
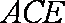
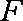
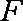
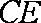
(1)求证:
(2)求四棱锥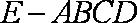
(3)设点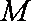
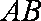
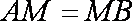
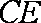
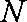
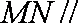
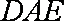
正确答案
见解析。
解析
(1)因为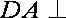
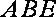
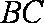
所以
因为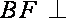
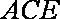
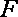

因为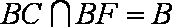
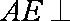
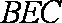
则
因为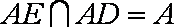
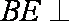
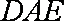
则

(2)
作

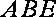
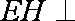
因为
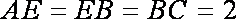
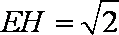

(3)因为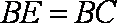
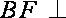
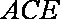
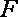
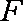
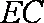
设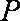
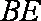
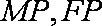
所以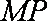
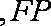
因为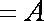
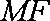
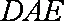
知识点
如图, 在直三棱柱ABC-A1B1C1中,AC=3,BC=4,AA1=4,AB=5. 点D是AB的中点,
(1)求证:AC⊥BC1;
(2)求证:AC 1//平面CDB1;
(3)求异面直线 AC1与 B1C所成角的余弦值。
正确答案
见解析。
解析
(1)直三棱柱ABC-A1B1C1,底面三边长AC=3,BC=4,AB=5,
∴ AC⊥BC,
又因为 
又 





(2)
设CB1与C1B的交点为E,连结DE,∵ D是AB的中点,E是BC1的中点
∵ DE


(3)∵ DE//AC1,∴ ∠CED为AC1与B1C所成的角,
在△CED中,ED=





∴ 
∴ 异面直线 AC1与 B1C所成角的余弦值
知识点
如图所示,PA⊥平面ABCD,ABCD是矩形,AB = 1,
(1)若

(2)若二面角



正确答案
见解析
解析
(1)证明:

∴
又


又

∴

∴

而

(2)由(1)知:

∴


∴
∴

即


知识点
如图,在底面为直角梯形的四棱锥





(1)求证:
(2)当
正确答案
见解析。
解析
(1)证明:由题意知

(2)



过D作DH⊥BC于点H,连结PH,则同理可证明
并且

易得


故此四棱锥的表面积

知识点
如图所示,圆柱的高为2,底面半径为


(1)求证
(2)求四棱锥E-ABCD的体积。
正确答案
见解析。
解析
(1)证明:



又







(2)因为母线


由(1)知






过



又







设正方形


又

在



知识点
19.如图,在四棱锥P-ABCD的底面是边长为2的正方形,PD⊥平面ABCD, E、F分别是PB、AD的中点,PD=2.
(I)求证:BC⊥PC;
(II)求证:EF//平面PDC;
(III)求三棱锥B—AEF的体积.
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
5.设






正确答案
解析
解析已在路上飞奔,马上就到!
知识点
19. 如图所示,在棱长为2的正方体





(Ⅰ)求证:

(Ⅱ)求证:
(Ⅲ)求
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
扫码查看完整答案与解析