- 立体几何与空间向量
- 共2637题
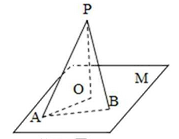
18.如图,四棱锥




(I)证明:
(II)设

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
4. 已知平面


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
15. 如图,直线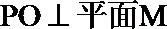

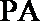
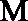
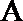
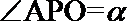
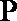
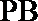

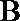
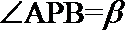
①若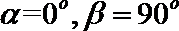
②若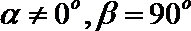
③若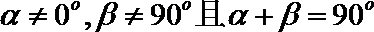
④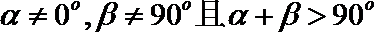
⑤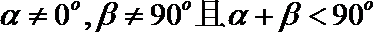
正确答案
②③
解析
解析已在路上飞奔,马上就到!
知识点
15.已知三棱锥P-ABC的底面是边长为3的等边三角形,PA⊥底面ABC,PA =2,则三棱锥P-ABC外接球的表面积为________。
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
17.如图,







(1)求证:
(2)设


(3)设平面


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
17.已知在四棱锥P - ABCD中,底面 ABCD是矩形,
(1)求证:AF
(2)求三棱锥B-PEC的体积;
(3)求证:AF//平面PEC
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
15.在三棱锥A—A′B′C′中,已知AA′⊥平面ABC,AA′=2,BC=

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
19. 如图,四棱柱ABCD-A1B1C1D1的底面ABCD是平行四边形,且AA1⊥底面ABCD,AB=2,AA1=BC=4,∠ABC=60°,点E为BC中点,点F为B1C1中点.
(Ⅰ)求证:平面A1ED⊥平面A1AEF;
(Ⅱ)求三棱锥E-A1FD的体积.
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
5.设






正确答案
解析
解析已在路上飞奔,马上就到!
知识点
8.设m,n是不同的直线,


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
19. 在直三棱柱






(1)当


(2)若

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
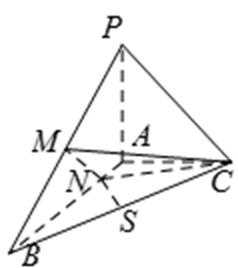
18.已知三棱锥PABC中,PA⊥平面ABC,AB⊥AC,PA=AC=AB,N为AB上一点,AB=4AN,M,S分别为PB,BC的中点.
(1)证明:CM⊥SN;
(2)求SN与平面CMN所成角的大小.
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
18. 如图,在三棱锥P-ABC中,PA
(I)证明:平面PBE
(II)在BC上找一点F,使AD∥平面PEF,并说明理由;
(III)在(II)的条件下,若PA=AB=2,求三棱锥B-PEF的体积.
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
4.设a,b是两条直线,α,β是两个平面,则
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
18.如图,正方形






(Ⅰ)若

(Ⅱ)求证:

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
扫码查看完整答案与解析