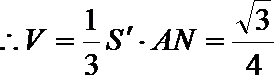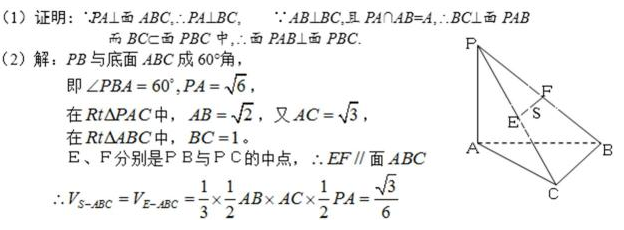立体几何与空间向量_章节学习

1

题型：填空题

|

填空题 · 4 分

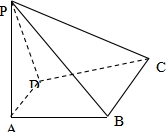
14. 如图所示，四棱锥中，底面是边长为的菱形，棱，．有下列命题：

① 若是的中点，则平面；

② 若，则；

③ 若是正三角形，则平面；

④ 若，，则四棱锥的体积为.

其中正确的命题是（）.

正确答案

①②④

解析

解析已在路上飞奔，马上就到！

知识点

命题的真假判断与应用棱柱、棱锥、棱台的体积直线与平面平行的判定与性质直线与直线垂直的判定与性质直线与平面垂直的判定与性质

1

题型：简答题

|

简答题 · 12 分

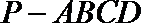
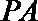
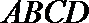
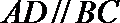
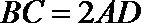
19. 如图，已知四棱锥中，⊥平面，是直角梯形，，90º，．

（1）求证：⊥；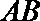

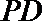
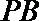
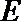
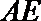
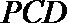
（2）在线段上是否存在一点，使//平面，若存在，指出点的位置并加以证明；若不存在，请说明理由。

正确答案

（1），BC=2，，， ∴，

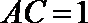
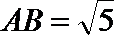
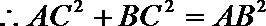
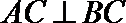
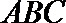
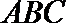
又∵平面PAC⊥平面，平面PAC∩平面=AC,

∴BC⊥平面PAC

又∵PA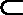平面PAC ∴PA⊥BC

（2）取PC的中点N，连接AN，由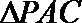是边长为1的正三角形，可知AN⊥PC，由（1）BC⊥平面PAC，可知AN⊥BC，∴AN⊥平面PCBM，

∴AN是四棱锥A—PCBM的高且AN= ，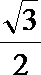

由BC⊥平面PAC，可知BC⊥PC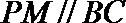，可知四边形PCBM是上、下底边长分别为1和2，PC的长1 为高的直角梯形，其面积

解析

解析已在路上飞奔，马上就到！

知识点

直线与平面平行的判定与性质直线与直线垂直的判定与性质直线与平面垂直的判定与性质

1

题型：简答题

|

简答题 · 12 分

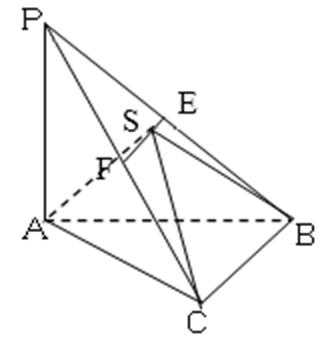
20．如图1，在直角梯形中, 将沿折起，使平面ADC平面ABC,得到几何体D－ABC, 如图2所示。

（Ⅰ）若E为AD的中点，试在线段CD上找一点F，使EF∥平面ABC，并加以证明；

（Ⅱ）求证: BC⊥平面ACD；

（Ⅲ）求几何体A－BCD的体积。

正确答案

（Ⅰ）在CD上中点F, 使EF∥平面ABC（略）

（Ⅱ）在图1中,可得,从而,故，

取中点连结,则,又面面,面面,面,从而平面,

∵面,∴

又,

∴平面

另解：在图1中,可得, 从而, 故

∵面面,面面,面,从而平面[来源:学§科§网]

（Ⅲ）由（Ⅰ）可知为三棱锥的高，

所以 ∴几何体的体积为

解析

解析已在路上飞奔，马上就到！

知识点

棱柱、棱锥、棱台的体积直线与平面平行的判定与性质直线与平面垂直的判定与性质

1

题型：简答题

|

简答题 · 12 分

17．三棱锥P−ABC中，PA⊥平面ABC，AB⊥BC。

（1）证明：平面PAB⊥平面PBC；

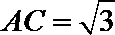
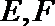
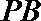
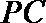
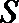
（2）若，，PB与底面ABC成60°角，分别是与的中点，是线段上任意一动点（可与端点重合），求多面体的体积。

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

组合几何体的面积、体积问题直线与平面垂直的判定与性质平面与平面垂直的判定与性质线面角和二面角的求法

1

题型：简答题

|

简答题 · 13 分

20．在如图所示的多面体ABCDE中，AB⊥平面ACD，DE⊥平面ACD，且AC=AD=CD=DE=2，AB=1

（1）请在线段CE上找到点F的位置，使得恰有直线BF∥平面ACD，并证明这一事实；

（2）求多面体ABCDE的体积；

（3）求直线EC与平面ABED所成角的正弦值。

正确答案

（1）

如图，由已知AB⊥平面ACD，DE⊥平面ACD，

∴AB//ED，

设F为线段CE的中点，H是线段CD的中点，

连接FH，则，∴，

∴四边形ABFH是平行四边形，

∴，

由平面ACD内，平面ACD，

平面ACD

（2）取AD中点G，连接CG．

AB平面ACD，

∴CGAB

又CGAD

∴CG平面ABED，即CG为四棱锥的高， CG=

∴=2=．

（3）连接EG，由（2）有CG平面ABED，

∴即为直线CE与平面ABED所成的角，

设为，则在中，

有．

解析

解析已在路上飞奔，马上就到！

知识点

组合几何体的面积、体积问题直线与平面平行的判定与性质直线与平面垂直的判定与性质线面角和二面角的求法

1

题型：简答题

|

简答题 · 14 分

19．如图，四棱锥P﹣ABCD，PA⊥底面ABCD，AB∥CD，AB⊥AD，AB=AD=CD=2，PA=2，E，F分别是PC，PD的中点．

（Ⅰ）证明：EF∥平面PAB；

（Ⅱ）求直线AC与平面ABEF所成角的正弦值．

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

直线与平面平行的判定与性质直线与平面垂直的判定与性质线面角和二面角的求法

1

题型：简答题

|

简答题 · 12 分

18．已知某几何体的直观图和三视图如下图所示，其正视图为矩形，侧视图为等腰直角三角形，俯视图为直角梯形。

（1）证明：BN⊥平面C1B1N；

（2）求点

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

简单空间图形的三视图直线与平面垂直的判定与性质

1

题型：简答题

|

简答题 · 12 分

20．如图，已知在直四棱柱ABCD-A1B1C1D1中，，AB//DC，DC=DD1=2AD=2AB=2。

（1）求证：平面B1BCC1；

（2）设E是DC上一点，试确定E的位置，使得D1E//平面A1BD，并说明理由。

正确答案

（1）设是的中点，连结，

则四边形为正方形，

．故，

，，

，即．

又，

平面，

（2）证明：DC的中点即为E点，

连D1E，BE

∴四边形ABED是平行四边形，

∴ADBE，又ADA1D1

A1D1

∴四边形A1D1EB是平行四边形

D1E//A1B ，

∵D1E平面A1BD

∴D1E//平面A1BD

解析

解析已在路上飞奔，马上就到！

知识点

直线与平面平行的判定与性质直线与平面垂直的判定与性质

1

题型：简答题

|

简答题 · 12 分

19．如图，四棱锥的底面是边长为8的正方形，四条侧棱长均为交于O点，点G，E，F，H分别是棱PB，AB，CD，PC上共面的四点，平面平面平面GEFH．

（I）证明：平面ABCD；

（II）GH//EF；

（III）若，求四边形GEFH的面积．

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

直线与直线平行的判定与性质直线与平面平行的判定与性质直线与平面垂直的判定与性质平面与平面垂直的判定与性质

1

题型：单选题

|

单选题 · 5 分

5．已知为不同的直线，为不同的平面，则下列说法正确的是（）

A

B

C

D

正确答案

D

解析

解析已在路上飞奔，马上就到！

知识点

命题的真假判断与应用直线与平面平行的判定与性质平面与平面平行的判定与性质直线与平面垂直的判定与性质平面与平面垂直的判定与性质

1

题型：单选题

|

单选题 · 5 分

7．如图所示，三棱锥满足平面，，，如果三棱锥的所有顶点都在球的表面上，则球的表面积为（）

A

B

C

D

正确答案

C

解析

解析已在路上飞奔，马上就到！

知识点

球的体积和表面积与球体有关的内切、外接问题直线与平面垂直的判定与性质

1

题型：单选题

|

单选题 · 5 分

10．如图，在等腰梯形中，分别是底边的中点，把四边形沿直线折成直二面角，若点平面，设与平面所成的角分别为（均不为0．若，则点的轨迹为（）

A直线

B圆

C椭圆

D抛物线

正确答案

B

解析

解析已在路上飞奔，马上就到！

知识点

直线与平面垂直的判定与性质线面角和二面角的求法

1

题型：简答题

|

简答题 · 14 分

21．如图，在四棱锥中，底面四边长为的菱形，，，，为的中点，为的中点

（1）证明：直线；

（2）求异面直线与所成角的大小；

正确答案

方法一（综合法）

（1）取OB中点E，连接ME，NE

又

（2）

为异面直线与所成的角（或其补角）作

连接

，

所以与所成角的大小为

方法二（向量法）作于点P，

如图，分别以AB，AP，AO所在直线为轴建立坐标系，

，

（1）

设平面OCD的法向量为，则n·，n·

即取，解得

（2）设与所成的角为，

，

与所成角的大小为

解析

解析已在路上飞奔，马上就到！

知识点

异面直线及其所成的角直线与平面平行的判定与性质直线与平面垂直的判定与性质

1

题型：简答题

|

简答题 · 12 分

19．如图，在三棱锥A—BOC中，平面COB，在中，OB=OC=1，，D、E分别为AB、BO的中点．

（I）求证：平面ABO；

（II）在线段CB上是否存在一点F，使得在CO上任取一点G均有AG//平面DEF？若存在，试确定F的位置；若不存在，请说明理由．

正确答案

（I）证明：因为平面BOC，OC在平面BOC内，所以OC；

因为OB＝OC＝1，BC＝2，所以，所以OCOB；

因为AO与BO相交于点O，所以CO垂直于平面AOB。

（II）适合条件的点F在在，且F是BC的中点，证明如下：

取BC的中点F，连结DF、EF。

因为D是OB的中点，所以DF//OC，同理，EF//AC，所以平面DEF//平面AOC。

因为AG在平面AOC内，所以AG//平面DEF。

解析

解析已在路上飞奔，马上就到！

知识点

直线与平面平行的判定与性质直线与平面垂直的判定与性质

1

题型：简答题

|

简答题 · 12 分

17．如图所示,矩形中，平面，为上的点，且平面交与点．

（1）求证：平面；

（2）求证：平面；

（3）求三棱锥的体积．

正确答案

（1）略;

（2）略;

（3）．

解析

解析已在路上飞奔，马上就到！

知识点

棱柱、棱锥、棱台的体积直线与平面平行的判定与性质直线与平面垂直的判定与性质

热门试卷

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点