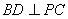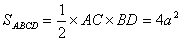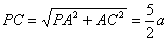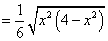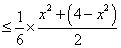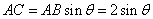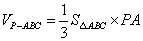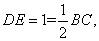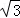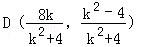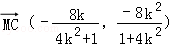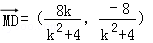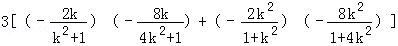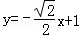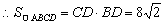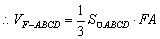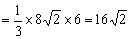- 立体几何与空间向量
- 共2637题
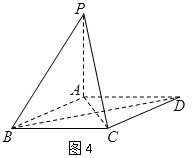
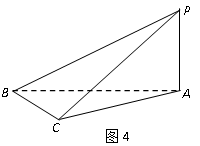
如图4,四棱锥
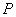
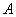
(1)求证: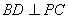
(2)若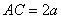
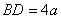
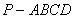
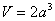
正确答案
见解析。
解析
(1)依题意,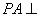
因为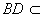
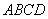
依题意,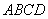
因为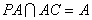
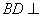
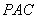
⑵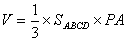
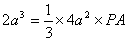
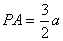
知识点
已知直线
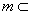
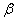
①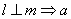
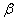

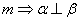
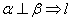
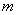
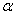
正确答案
解析
略
知识点
已知直线
正确答案
解析
略
知识点
已知直线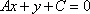


正确答案
解析
∵
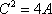





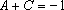
知识点
在如图所示的棱长为


正确答案

解析
略
知识点
某几何体的三视图如图所示,则该几何体外接球的表面积为
正确答案
解析
略
知识点
如图4, 在三棱锥
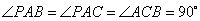
(1)求证:平面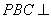
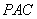
(2)若
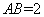
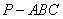
求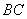
正确答案
见解析。
解析
(1)证明:因为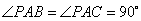

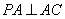
因为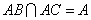
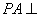
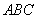
因为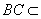
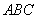
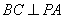
因为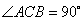
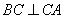
因为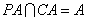
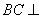
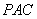
因为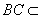
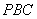
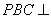
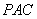
(2)
方法1:由已知及(1)所证可知,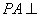
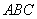
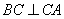
所以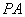

因为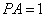
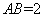
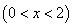
所以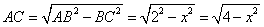
因为
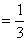
当且仅当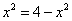
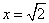
所以当三棱锥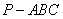
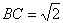
方法2:由已知及(1)所证可知,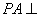
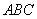
所以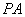

因为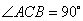
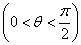
则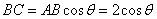
所以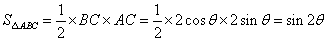
所以
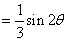
因为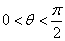
所以当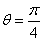
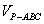
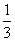
此时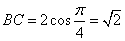
所以当三棱锥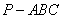
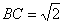
知识点
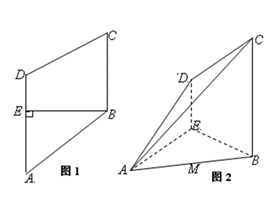
如图2所示,已知四棱锥P–ABCD的底面是直角梯形,∠ABC=∠BCD = 90°,AB = BC = PB = PC = 2CD,侧面PBC⊥底面ABCD。
(1)证明:PA⊥BD;
(2)求二面角P – BD – C的大小;
(3)求证:平面PAD⊥平面PAB。
正确答案
见解析。
解析
解法一:
(1)取BC中点O,连结AO交BD于点E,连结PO
∵PB = PC,∴PO⊥BC
又∵平面PBC⊥平面ABCD,平面PBC∩平面ABCD = BC
∴PO⊥平面ABCD
在直角梯形ABCD中
∵AB = BC = 2CD,易知Rt△ABO≌Rt△BCD
∴∠BEO =∠OAB +∠DBA =∠DBC +∠DBA = 90°
即AO⊥BD,由三垂线定理知PA⊥BD。
(2)连结PE,由PO⊥平面ABCD,AO⊥BD
得PE⊥BD
∴∠PEO为二面角P – BD – C的平面角
设AB = BC = PB = PC = 2CD = 2a
则PO =
在Rt△PEO中,tan∠PEO =
∴二面角P – BD– C的大小为arctan
(3)取PB的中点为N,连结CN,则CN⊥PB
又∵AB⊥BC,BC是PB在面ABCD内的射影
∴AB⊥PB,又PB∩BC = B
∴AB⊥面PBC,∴平面PAB⊥平面PBC
∵CN⊥PB,面PAB∩面PBC = PB
∴CN⊥平面PAB
取PA的中点为M,连结DM、MN
则MN∥AB∥CD,∵MN =
∴四边形MNCD为平行四边形
∴CN∥DM,∴DM⊥平面PAB
∴平面PAD⊥平面PAB。
解法二:
(1)取BC中点为O
∵侧面PBC⊥底面ABCD,△PBC为等边三角形
∴PO⊥底面ABCD,以BC的中点O为坐标原点,以BC所在直线为x轴,过点O与AB平行的直线为y轴,直线OP为z轴,如图乙所示,建立空间直角坐标系。
不妨设CD = 1
则AB = BC = PB = PC = 2,PO =
∴A(1,– 2,0),B (1,0,0),D (– 1,– 1,0),P (0,0,
∴


∵


∴

(2)连结AO,设AO与BD相交于点E,连结PE
由

∴

又∵EO为PE在平面ABCD内的射影,∴PE⊥BD
∴∠PEO为二面角P – BD – C的平面角
在Rt△BEO中,OE = OB · sin∠OBE =
∴在Rt△PEO中,tan∠PEO =
∴二面角P – BD – C的大小为arctan
(3)取PA的中点M,连结DM
则M
∴


∴

又∵

∴


∴

∴平面PAD⊥平面PAB。
知识点
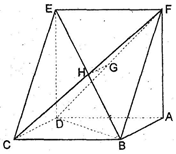
如图:已知长方体








(1)求证:

(2)求证:

(3)求三棱锥
正确答案
见解析
解析
(1)









(2)连结






又




(3)


同样计算可得







知识点
如图5,在平行四边形ABCD中,∠A=90°,∠B=135°,∠C=60°,AB=AD,M,N分别是边AB,CD上的点,且2AM=MD,2CN=ND,如图5,将△ABD沿对角线BD折叠,使得平面ABD⊥平面BCD,并连结AC,MN(如图6)。
(1)证明:MN∥平面ABC;
(2)证明:AD⊥BC;
(3)若BC=1,求三棱锥A-BCD的体积。
正确答案
见解析。
解析
知识点
如图1,在梯形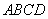
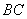
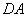
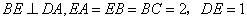
将四边形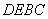
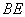
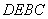
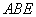
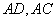
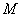
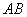
(1)若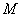
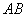
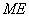
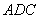
(2)若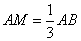
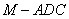
正确答案
见解析。
解析
(1)取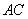
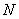
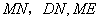
∵ 
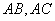
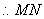
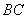
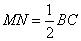
又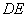
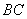
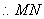
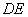
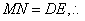
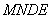
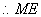
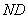
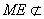
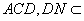
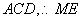
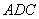
(2)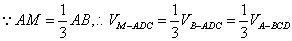

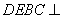
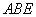
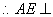
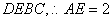
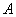
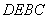
又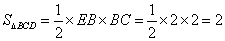
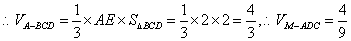
知识点
如图,AD

(1)求证:AF∥平面BDE;
(2)求证:平面BDE
正确答案
见解析。
解析
(1)证明:∵AD⊥平面ABC,AC

∴AD⊥AC,AD⊥AB,
∵AD∥CE,∴CE⊥AC
∴四边形ACED为直角梯形.……………(1分)
又∵∠BAC=90°,∴AB⊥AC,∴AB⊥面ACED.
………………(2分)
∴凸多面体ABCED的体积
求得CE=2.……………………………………………………(3分)
取BE的中点G,连结GF,GD,
则GF∥EC,GF
∴GF∥AD,GF=AD,四边形ADGF为平行四边形,
∴AF∥DG.………………………………………………………(5分)
又∵GD

∴AF∥平面BDE.………………………………………………(7分)
(2)证明:∵AB=AC,F为BC的中点,
∴AF⊥BC.………………………………………………………(8分)
由(1)知AD⊥平面ABC,AD∥GF,∴GF⊥面ABC.
∵AF
又BC
又∵DG∥AF,∴DG⊥面BCE.……………………………(11分)
∵DG
知识点
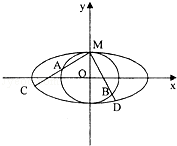
如图,圆O与离心率为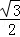
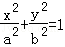
(1)求椭圆T与圆O的方程;
(2)过点M引两条互相垂直的两直线l1、l2与两曲线分别交于点A、C与点B、D(均不重合)。
①若P为椭圆上任一点,记点P到两直线的距离分别为d1、d2,求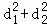
②若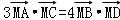
正确答案
见解析。
解析
(1)由题意知: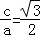
又a2=b2+c2,所以a2=c2+1,
联立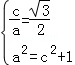
所以椭圆C的方程为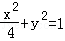
(2)①设P(x0,y0)因为l1⊥l2,则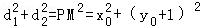
因为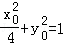
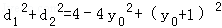
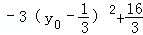
因为﹣1≤y0≤1,所以当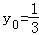
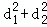
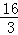
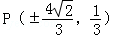
②设l1的方程为y=kx+1,
由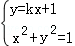
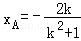
代入y=kx+1得: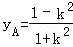
所以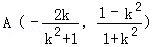
由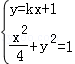
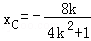
代入y=kx+1得: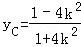
所以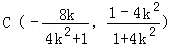
把A,C中的k置换成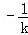
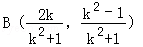
所以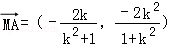
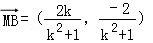
由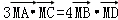
得
=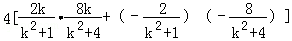
整理得: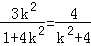
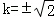
所以l1的方程为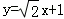
或l1的方程为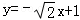
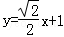
知识点
已知如图:平行四边形ABCD中,BC=6,正方形ADEF所在平面与平面ABCD垂直,G,H分别是DF,BE的中点。
(1)求证:GH∥平面CDE;
(2)若CD=2,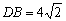
正确答案
见解析。
解析
(1)证法:∵EF//AD, AD//BC ∴EF//BC且EF=AD=BC
∴四边形EFBC是平行四边形 ∴H为FC的中点
又∵G是FD的中点
∴HG//CD
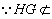
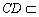
∴GH//平面CDE
证法2:连结EA,∵ADEF是正方形 ∴G是AE的中点
∴在△EAB中,GH//AB
又∵AB//CD,∴GH//CD,
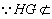
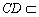
∴GH//平面CDE
(2)∵平面ADEF⊥平面ABCD,交线为AD
且FA⊥AD, ∴FA⊥平面ABCD,
∵BC=6, ∴FA=6 又∵CD=2,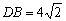
∴BD⊥CD
知识点
如图,在四棱锥












(1)若



(2)求证:平面

(3)是否存在点


写出证明过程并求出线段
正确答案
见解析
解析
(1)因为

所以 
因为

而



所以

(2)因为平面

平面




所以




又因为



而

所以平面

(3)存在点


在棱


由已知,



由平面几何知识可得 
由(2)知,


因为


而


又因为


在

可求得,
可见直线



知识点
扫码查看完整答案与解析