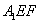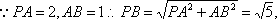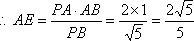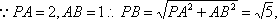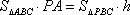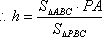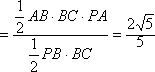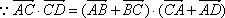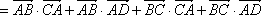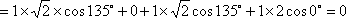- 立体几何与空间向量
- 共2637题
把三阶行列式



正确答案
解析
略
知识点
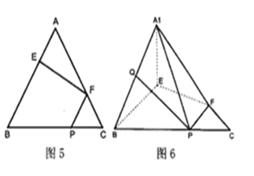
如图5,在边长为3的等边三角形ABC中,E,F,P分别为AB,AC,BC边上的点,且满足AE=FC=CP=1,将
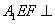
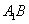
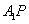
(1)求证: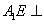
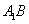
正确答案
见解析。
解析
知识点
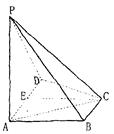
如图6,已知四棱锥P-ABCD中
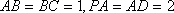
(1)求PC与平面PAB所成角的正切值;
(2)求证:平面PAC⊥平面PCD.
正确答案
见解析。
解析
(1)解法一:∵PA⊥平面ABCD,BC 
又∵BC⊥AB,PA∩AB=A ∴BC⊥平面PAB
又∵BC
在平面PAB内过点A作AE⊥PB于E,则AE⊥平面PBC,
∴AE的长为点A到与平面PAC的距离
在Rt△PAB
解法二:∵PA⊥平面ABCD,AD 
又∵DA⊥AB,PA∩AB=A ∴AD⊥平面PAB
∵BC⊥AB ∴BC∥AD ∴BC⊥平面PAB ∴BC⊥PB
在Rt△PAB
设点A到平面PBC的距离为h,则由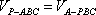
(2)证法一:
过点C作CE∥AB交AD于点E,
∵DA⊥AB ∴DA⊥EC,且AE =BC =1
∵AD =2,∴E为AD的中点,∴EC为AD的垂直平分线,
∴CD=AC,∵△ABC为等腰直角三角形,∴∠BAC=450
∴∠DAC =∠ADC=450,∴∠DCA=900,即DC⊥AC,
又∵PA⊥平面ABCD,CD
且PA∩AC=A,
∴CD⊥平面PAC,∵CD
∴平面PAC⊥平面PCD
证法二:∵PA⊥平面ABCD,CD
又
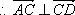
又∵PA⊥平面ABCD,CD
∴CD⊥平面PAC,∵CD
∴平面PAC⊥平面PCD.
知识点
如图1,在直角梯形








(1) 求证:


正确答案
见解析。
解析
解:(1)在图1中,可得

取





面





∴
又

∴
另解:在图1中,可得

∵面ACD






(2) 由(1)可知


所以
由等积性可知几何体
知识点
如图,在梯形









(1)求证:

(2)当FM为何值时,AM
正确答案
见解析。
解析
(1)由题意知,


所以
又平面



所以

(2)
当


在梯形



因为

所以

所以四边形

又



所以

知识点
已知复数

正确答案
2
解析
略
知识点
如图,在四棱锥







(1)当




(2)求证:平面

正确答案
见解析
解析
(1)连接


因为



所以

(2)证明:由已知可得,


所以
又因为四边形

因为

又因为


知识点
如图,已知四棱锥



(1)求三棱锥
(2)求异面直线

正确答案
(1)
解析
解析:(1)

(2)









知识点
如图,棱柱



(1)求证:平面

(2)设






正确答案
见解析
解析
解析:(1)证明:


故



(2)记















因为底面
则



故


知识点
如图,平面ABDE⊥平面ABC,AC


(1)证明:OD//平面ABC;
(2)能否在EM上找一点N,使得ON⊥平面ABDE?若能,请指出点N的位置,并加以证明;若不能,请说明理由。
正确答案
见解析。
解析
(1)证明:
取AC中点F,连结OF、FB.
∵F是AC的中点,O为CE的中点,
∴OF∥EA且OF=

∴OF∥DB,OF=DB,
∴四边形BDOF是平行四边形。
∴OD∥FB …………4分
又∵FB

(II)当N是EM中点时,ON⊥平面ABDE。 ………7分
证明:取EM中点N,连结ON、CM, AC=BC,M为AB中点,∴CM⊥AB,
又∵面ABDE⊥面ABC,面ABDE

∴CM⊥面ABDE, ∵N是EM中点,O为CE中点,∴ON∥CM,
∴ON⊥平面ABDE。 …………12分
知识点
如图,已知矩形






(1)求证:

(2)求多面体
(3)求多面体
正确答案
见解析。
解析
(1)连接



在矩形









(2)由题设和图形易知:



……………8分

(3)过点






即







知识点
如图,三棱柱ABC—A1B1C1的侧面AA1B1B为正方形,侧面BB1C1C菱形,∠CBB1=60°,AB⊥B1C。
(1)求证:平面AA1B1B⊥平面BB1C1C;
(2)若AB=2,求三棱柱ABC—A1B1C1体积。
正确答案
见解析
解析
(1)由侧面AA1B1B为正方形,知AB⊥BB1。
又AB⊥B1C,BB1∩B1C=B1,所以AB⊥平面BB1C1C,
又AB平面AA1B1B,所以平面AA1B1B⊥BB1C1C, …4分
(2)由题意,CB=CB1,设O是BB1的中点,连结CO,则CO⊥BB1。
由(1)知,CO⊥平面AB1B1A,且CO=BC=AB=,
连结AB1,则VC-ABB1=S△ABB1·CO=AB2·CO=, …8分
因VB1-ABC=VC-ABB1=VABC-A1B1C1=,
故三棱柱ABC-A1B1C1的体积VABC-A1B1C1=2. …12分
知识点
如图,四棱锥P-ABCD的底面ABCD为矩形,且PA=AD=1,AB=2, 

(1)求证:平面

(2)求三棱锥D-
正确答案
见解析。
解析
(1)证明:∵ABCD为矩形
∴
∵

∴


∴平面
(2) ∵
由(1)知




∴
知识点
如图,在四棱锥P—ABCD中,底面ABCD是正方形,PD⊥底面ABCD,M、N分别为PA、BC的中点,且PD=AD
(1)求证:MN//平面PCD;
(2)求证:平面PAC⊥平面PBD;
正确答案
见解析。
解析
(1)
取AD中点E,连接ME,NE. www.zxxk.com
由已知M,N分别是PA,BC的中点.
∴ME//PD,NE//CD……………………………………2分
又ME,

所以,平面MNE//平面PCD.…………………………4分
MN
所以,MN//平面PCD………………………………6分
(2)因为四边形ABCD为正方形.
所以AC⊥BD.
又PD⊥平面ABCD.AC
又BD
所以AC⊥平面PBD.…
AC
所以平面PAC⊥平面PBD…………………………………………………………12分
知识点
在等腰梯形




沿AD折起,使得

图2中完成下面问题:
(1)证明:平面
(2)在线段



若不存在,请说明理由.
正确答案
见解析。
解析
(1)∵在图1的等腰梯形

∴所以在四棱锥

又



而




∴



∴平面

(2)当


证明:在梯形



连结



又



又因为





知识点
扫码查看完整答案与解析