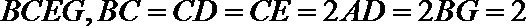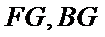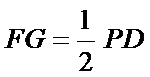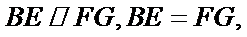- 立体几何与空间向量
- 共2637题
4.已知



正确答案
解析
解析已在路上飞奔,马上就到!
知识点
17.如图,已知四边形ABCD和BCEG均为直角梯形,AD//BC,CE//BG,且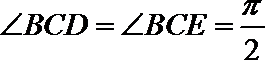
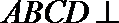
求证:(I)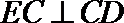
(II)求证: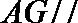
(III)求:几何体EG-ABCD的体积。
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
12.四棱锥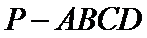
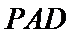
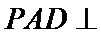
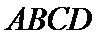
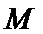
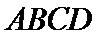

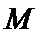
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
15.若l,m为空间两条不同的直线,


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
18.如图,在直三棱柱


(1)求证:EF∥平面ABC;
(2)求证:平面

(3)若

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
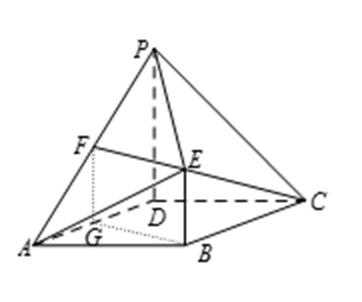
19.如图,四棱锥



(I)证明:
(II)GH//EF;
(III)若
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
17.如图,在四棱柱ABCD﹣A1B1C1D1中,AB=BC=CA=
(Ⅰ)求证:BD⊥AA1;
(Ⅱ)求证:A1E∥平面DCC1D1
(Ⅲ) 若AA1⊥AC,求A1E与面ACC1A1所成角大小.
正确答案
(Ⅰ)证明:在四棱锥ABCD﹣A1B1C1D1中,
∵AB=BC=CA,且AD=DC,
取AC中点O,则BO⊥AC,DO⊥AC,∴B,O,D三点在一条直线上.
又∵面AA1C1C⊥面ABCD,面AA1C1C∩面ABCD=AC,BD⊂面ABCD,BD⊥AC,
∴BD⊥面AA1C1C,AA1⊂面AA1C1C,∴BD⊥AA1;
(Ⅱ)证明:连AE,在Rt△DCO中∠DCO=30°
在正△BCA中,∠BCO=60°,∴DC⊥BC,
又在正△BCA中,AE⊥BC,
∴AE∥DC,
又AE⊄面DCC1D1,DC⊂面DCC1D1,∴AE∥面DCC1D1,
在四棱锥中,AA1∥DD1,AA1⊄面DCC1D1,DD1⊂面DCC1D1,
∴AA1∥面DCC1D1,
又AA1∩AE=A,
∴面A1AE∥面DCC1D1,
又A1E⊂面AA1E,故A1E∥面DCC1D1.
(Ⅲ)解:过E作AC的垂线,设垂足为N,∵面ABCD⊥面AA1C1C,∴EN⊥面AA1C1C,
连A1N,则A1N为A1E在面AA1C1C内的射影,
∴∠EA1N为直线A1E与面AC1所成角,
由已知得:

解析
解析已在路上飞奔,马上就到!
知识点
5.已知

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
9.三棱锥P-ABC的三条侧棱PA、PB、PC两两互相垂直,且长度分别为3、4、5,则三棱锥P-ABC外接球的表面积是( )
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
16.如图,在四棱锥








(1)如果


(2)如果


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
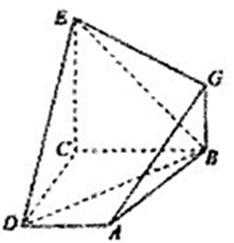
19.已知在四棱锥S—ABCD中,底面ABCD是平行四边形,若SB丄AC,SA = SC.(1)求证:平面SBD丄平面(2)若 AB = 2,SB = 3,cos∠SCB=
正确答案
如图所示
因为SA=SC,
所以SO∩SB=S,
所以AC⊥平面SBD,
因为AC在平面ABCD内,
所以平面SBD⊥平面ABCD
(2)⊥平面ABCD,即
由(1)知,AC⊥BD,所以底面ABCD是菱形,
所以BC=AB=2
因为SB=3,cos∠SCB=1/8
所以由余弦定理可得,SC=2,
所以∠SAC=60°,
所以SAC是等边三角形
所以在Rt△SOH中,SH=SO*sin60°=3/2
所以
解析
证AC垂直于面ABCD, 设AC交BD于0,因为SA=SC,SO交SB于S,所以AC垂直于平面SBD,因为AC在平面ABCD内,所以面SBD垂直于面ABCD.求底面面积时,先用余弦定理求出角SOB=120度,角SOH=60度,所以四棱锥的体积为
考查方向
立体几何中的相关计算和证明
解题思路
通过线线垂直得到线面垂直,进而得到面面垂直,找清四棱锥的底面和高,利用公式求解。
易错点
面面垂直概念混淆,立体感不强
知识点
19.如图,矩形CDEF和梯形ABCD互相垂直,∠BAD=∠ADC=90°,AB=AD=
正确答案
(1)略;(2)
解析
⑴证明:设






因为

所以

又因为



所以

⑵解:取









所以

同理

所以,



所以四边形

所以

又因为

所以
又

所以


注意到


所以
考查方向
本题考查了立体几何中的线面平行和体积.属于考中的高频考点。
解题思路
本题考查立体几何,解题步骤如下:
1、转化为证明线线平行。
2、利用体积公式求解。
易错点
第一问中的线面平行的转化。
知识点
19.如图,在四棱锥P-ABCD中,平面PAD⊥平面ABCD,E为AD上一点,F为PC上一点,四边形BCDE为矩形,∠PAD=60°,PB=2√3,PA=ED=2AE=2.(1)若




正确答案
见解析
解析
试题分析:本题属于立体几何中的基本问题,题目的难度是逐渐由易到难.
(1)连接



因为



所以
因为

因为

所以
(2)因为
所以
所以
又平面





(3)由(2)知,
∴ ∠PBE为直线PB与平面ABCD所成的角,
在RtΔPEB中,


直线PB与平面ABCD所成的角为60°.
考查方向
解题思路
本题考查立体几何中的线面位置关系,解题步骤如下:1、利用线面平行的性质定理。2、利用线面垂直的定义及判定定理转化。
易错点
1、第一问中的线线平行的判定。2、第二问中求证线面垂直时要与平面内的两条相交直线垂直。
知识点
15.半径为1的球面上有四个点





正确答案
解析
由题意可知图形如图所示,
AB过点



考查方向
解题思路
根据图中的有关关系,确定图形的特征,将三棱锥


易错点
本题容易因对球面上的问题想象不到位,不能很好地寻求分割图形的策略而导致错误的出现。
知识点
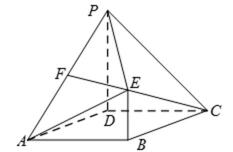
18. 如图,四边形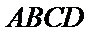
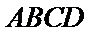
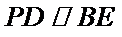
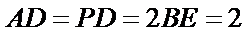
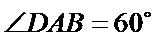
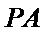
(Ⅰ)求证: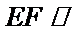
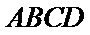
(Ⅱ)求证:平面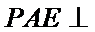
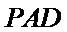
(Ⅲ)求三棱锥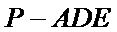
正确答案
(Ⅰ)略;
(Ⅱ)略;
(Ⅲ)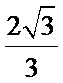
解析
(Ⅰ)取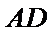
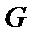
因为点
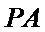
所以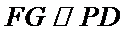
又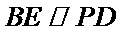
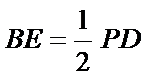
所以
所以四边形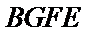
所以
又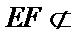
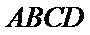
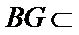
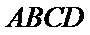
所以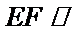
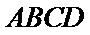
(Ⅱ)连接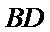
因为四边形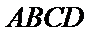
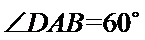

因为
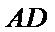
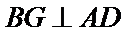
又因为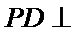
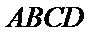
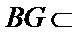
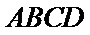
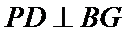
又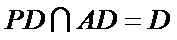
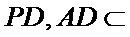
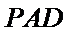
所以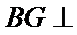
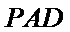
又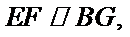
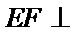
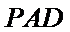
又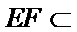
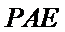
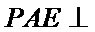
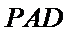
法二:因为四边形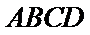
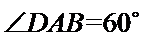
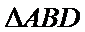
因为
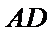
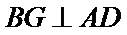
又因为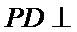
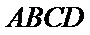
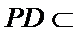
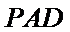
所以平面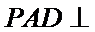
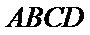
又平面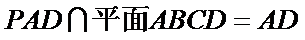
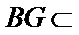
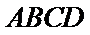
所以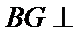
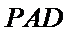
又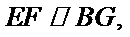
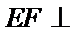
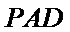
又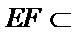
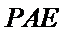
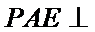

(Ⅲ)因为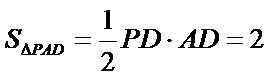
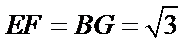
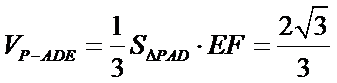
考查方向
本题考查了线面平行,面面垂直的证明,体积的求法,在近几年的各省高考题出现的频率非常高.
解题思路
(Ⅰ)借助于平行四边形,得到线线平行,进而得到线面平行;
(Ⅱ)利用面面垂直的判定定理;
易错点
定理记忆不清致误.
知识点
扫码查看完整答案与解析