立体几何与空间向量_章节学习

1

题型：填空题

|

填空题 · 4 分

14．用斜二测画法画一个边长为的正三角形的直观图，则此直观图面积的为_____.

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

直线、平面垂直的综合应用

1

题型：填空题

|

填空题 · 5 分

选做题（14 ～15题，考生只能从中选做一题）

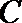
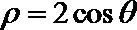
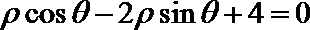
14．（坐标系与参数方程选做题）已知圆的极坐标方程为，则圆上点到直线的最短距离为（）。

15．（几何证明选讲选做题）如图，在中， //， //，若，则的长为（）．

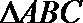
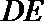
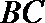
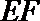
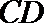
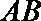
正确答案

14．

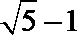
15．4

解析

解析已在路上飞奔，马上就到！

知识点

直线、平面垂直的综合应用

1

题型：简答题

|

简答题 · 12 分

21．如图,在四棱锥P-ABCD中,底面ABCD为菱形, ,Q为AD的中点

（1）若PA=PD,求证: 平面PQB平面PAD；

（2）点M在线段PC上，PM＝PC,试确定实数的值，使得PA//平面MQB。

正确答案

（1）依题意，可设故又

由余弦定理可知

＝3

∴

故可知，可知，

(另解:连结BD,由,AD=AB,可知ABD为等边三角形,又Q为AD的中点,所以也可证得)

又在中，PA=PD ，Q为AD的中点

∴，又

∴

又所以平面PQB平面PAD

（2）连结AC交BQ于点O ，连结MO，

欲使 PA//平面MQB

只需满足 PA//OM 即可

又由已知 AQ//BC

易证得 ∴

故只需，即时，满足题意

∵

∴可知 PA//OM 又

所以可知当时， PA//平面MQB

解析

解析已在路上飞奔，马上就到！

知识点

直线、平面垂直的综合应用

1

题型：填空题

|

填空题 · 5 分

12．，若，则的所有值为（）

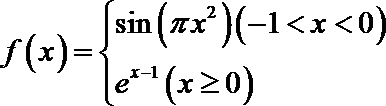
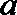
正确答案

解析

解析已在路上飞奔，马上就到！

知识点

直线、平面垂直的综合应用

1

题型：简答题

|

简答题 · 12 分

如图，正方形ABCD和直角梯形ACEF所在的平面互相垂直，,

正确答案

见解析。

解析

（1）设正方形的对角线与交于点，连接.由题知，

∵，∴四边形为平行四边形

∴

（2）

连，易知四边形为边长为1的正方形

∴

∴为等腰三角形，

∵

∴

同理在中，

知识点

直线、平面垂直的综合应用

1

题型：单选题

|

单选题 · 5 分

6．设是两条不同直线，是两个不同平面，则下列命题中正确的是（　　　）

A若，　则

B若，则

C若，则

D若，则

正确答案

D

解析

解析已在路上飞奔，马上就到！

知识点

直线、平面垂直的综合应用

1

题型：简答题

|

简答题 · 13 分

17．如图，已知四棱锥P－ABCD的底面是菱形，∠BCD＝60°，点E是BC边的中点，AC与DE交于点O，PO⊥平面ABCD.

（Ⅰ）求证：PD⊥BC；

（Ⅱ）若AB＝6，PC＝6，求二面角P－AD－C的大小；

（Ⅲ）在（Ⅱ）的条件下，求异面直线PB与DE所成角的余弦值．

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

直线、平面垂直的综合应用

1

题型：简答题

|

简答题 · 12 分

18.在几何体ABCDE中，∠BAC=，DC⊥平面ABC，EB⊥平面ABC，F是BC的中点，AB=AC=BE=2，CD=1

（Ⅰ）求证：DC∥平面ABE；

（Ⅱ）求证：AF⊥平面BCDE；

（Ⅲ）求证：平面AFD⊥平面AFE。

18．在几何体ABCDE中，∠BAC=，DC⊥平面ABC，EB⊥平面ABC，F是BC的中点，AB=AC=BE=2，CD=1

（Ⅰ）求证：DC∥平面ABE；

（Ⅱ）求证：AF⊥平面BCDE；

（Ⅲ）求证：平面AFD⊥平面AFE．

第(1)小题正确答案及相关解析

正确答案

1

题型：单选题

|

单选题 · 5 分

4．设l，m是两条不同的直线，α是一个平面，则下列命题正确的是（）

A若l⊥m，，则l⊥α

B若l⊥α，l∥m，则m⊥α

C若l∥α，，则l∥m

D若l∥α，m∥α，则l∥m

正确答案

B

解析

解析已在路上飞奔，马上就到！

知识点

直线、平面垂直的综合应用

1

题型：填空题

|

填空题 · 4 分

6．若满足，则目标函数取最大值时（）。

正确答案

4

解析

解析已在路上飞奔，马上就到！

知识点

直线、平面垂直的综合应用

1

题型：填空题

|

填空题 · 4 分

17．如图所示，在三棱柱ABC－A1B1C1中，AA1底面A1B1C1，底面为直角三角形，∠ACB＝90°，AC＝，BC＝CC1＝1，P是BC1上一动点，则A1P＋PC的最小值是_____．

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

直线、平面垂直的综合应用

1

题型：单选题

|

单选题 · 5 分

4．已知是两条不同的直线，是两个不同的平面，则下列命题中不正确的是（）

A若则

B若则

C若，则

D若，则

正确答案

D

解析

解析已在路上飞奔，马上就到！

知识点

直线、平面垂直的综合应用

1

题型：简答题

|

简答题 · 12 分

18．如图，在四棱锥中，底面为菱形，，为的中点。

（1）若，求证：平面平面；

（2）点在线段上，，试确定的值，使平面。

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

直线、平面垂直的综合应用

1

题型：简答题

|

简答题 · 13 分

21．已知某几何体的俯视图是如图所示的矩形，正视图（或称主视图）是一个底边长为8、高为4的等腰三角形，侧视图（或称左视图）是一个底边长为6、高为4的等腰三角形。

（1）求该几何体的体积V；

（2）求该几何体的侧面积S。

正确答案

由题设可知，几何体是一个高为4的四棱锥，

其底面是长、宽分别为8和6的矩形，

正侧面及其相对侧面均为底边长为8，

高为的等腰三角形，

左、右侧面均为底边长为6，

高为的等腰三角形．

（1）几何体的体积为为

．

（2）正侧面及相对侧面底边上的高为:

，

左、右侧面的底边上的高为:

．

故几何体的侧面面积为:

S = 2×（×8×5+×6×4）．

解析

解析已在路上飞奔，马上就到！

知识点

直线、平面垂直的综合应用

1

题型：简答题

|

简答题 · 14 分

16.如图，在棱长为2的正方体中，为的中点，为的中点。

（1）求证：；

（2）求三棱锥的体积。

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

直线、平面垂直的综合应用

热门试卷

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点