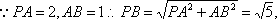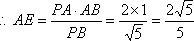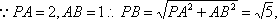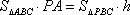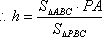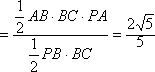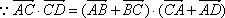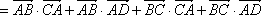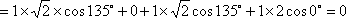- 立体几何与空间向量
- 共2637题
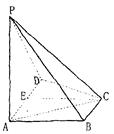
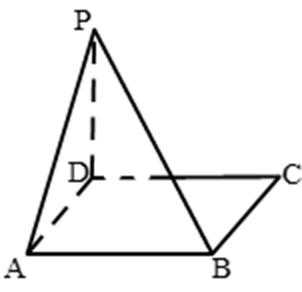
已知在四棱锥P﹣ABCD中,底面ABCD是矩形,PA⊥平面ABCD,AB=2,PA=AD=1,E,F分别是AB、PD的中点。
(1)求证:AF⊥平面PDC;
(2)求三棱锥B﹣PEC的体积;
(3)求证:AF∥平面PEC。
正确答案
见解析。
解析
(1)证明:∵PA⊥平面ABCD,∴PA⊥CD,
由底面ABCD是矩形,∴CD⊥DA,又PA∩AD=A,∴CD⊥平面PAD,
∴CD⊥AF。
∵PA=AD=1,F是PD的中点,
∴AF⊥PD,
又PD∩DC=D,∴AF⊥平面PDC。
(2)解:

∵PA⊥平面ABCD,
VB﹣PEC=VP﹣BEC=

(3)取PC得中点M,连接MF、ME。
∵


∴四边形AEMF是平行四边形,
∴AF∥EM。
又AF⊄平面PEC,EM⊂平面PEC,
∴AF∥平面PEC。
知识点
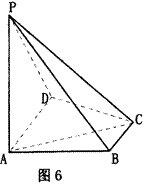
如图6,已知四棱锥P-ABCD中
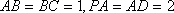
(1)求PC与平面PAB所成角的正切值;
(2)求证:平面PAC⊥平面PCD.
正确答案
见解析。
解析
(1)解法一:∵PA⊥平面ABCD,BC 
又∵BC⊥AB,PA∩AB=A ∴BC⊥平面PAB
又∵BC
在平面PAB内过点A作AE⊥PB于E,则AE⊥平面PBC,
∴AE的长为点A到与平面PAC的距离
在Rt△PAB
解法二:∵PA⊥平面ABCD,AD 
又∵DA⊥AB,PA∩AB=A ∴AD⊥平面PAB
∵BC⊥AB ∴BC∥AD ∴BC⊥平面PAB ∴BC⊥PB
在Rt△PAB
设点A到平面PBC的距离为h,则由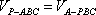
(2)证法一:
过点C作CE∥AB交AD于点E,
∵DA⊥AB ∴DA⊥EC,且AE =BC =1
∵AD =2,∴E为AD的中点,∴EC为AD的垂直平分线,
∴CD=AC,∵△ABC为等腰直角三角形,∴∠BAC=450
∴∠DAC =∠ADC=450,∴∠DCA=900,即DC⊥AC,
又∵PA⊥平面ABCD,CD
且PA∩AC=A,
∴CD⊥平面PAC,∵CD
∴平面PAC⊥平面PCD
证法二:∵PA⊥平面ABCD,CD
又
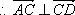
又∵PA⊥平面ABCD,CD
∴CD⊥平面PAC,∵CD
∴平面PAC⊥平面PCD.
知识点
如图,四棱锥


(1)平面PAD与平面PAB是否垂直?并说明理由;
(2)求直线PC与平面ABCD所成角的正弦值。
正确答案
见解析。
解析
(1)平面
∵
∵四棱锥

∵






∵




平面

(2)如图,过点




由(1)可知
∵
∴平面
∵



平面

∴
∴


∴






在直角三角形
故
在直角三角形

故直线


知识点
如图,在斜三棱柱






(1)求
(2)证明EA1∥平面
正确答案
见解析。
解析
(1)解:过










因为


又因为



因此,由三垂线定理
因为


于是为


由于四边形
所以,


(2) 证明:设


在平行四边形

而EP





知识点
如图所示,PA⊥平面ABCD,ABCD是矩形,AB = 1,
(1)若

(2)若二面角



正确答案
见解析
解析
(1)证明:

∴
又


又

∴

∴

而

(2)由(1)知:

∴


∴
∴

即


知识点
19.如图,在三棱锥P—ABC中,
(I)求证:
(II)求点A到平面PEF的距离;
(III)求二面角E—PF—A的正切值。
正确答案
: 解法一:
(I)
AD为PD在平面ABC内的射影。
又
在


(II)设EF与AD相交于点G,连接PG。


过A做AO
所以线段AO的长为点A到平面PEF的距离
在
即点A到平面PEF的距离为
说 明:该问还可以用等体积转化法求解,请根据解答给分。
(III)

过A做
则
所以
在
即二面角E—PF—A的正切值为
解法二:

则A(0,0,0),E(2,0,0),D(2,2,0),F(0,2,0),P(0,0,2)
(I)
且

(II)
则
令
故点A到平面PEF的距离
所以点A到平面PEF的距离为
(III)依题意
设二面角E—PF—A的大小为

则,
所以
即二面角E—PF—A的正切值为
解析
解析已在路上飞奔,马上就到!
知识点
9.已知圆锥的底面半径


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
17.在三棱锥




(1)求证:
(2)求二面角
(3)求点

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
20.如图所示,已知单位正方体


(1)求
(2)求异面直线

正确答案
(1)过E作EF⊥平面ABCD,F为垂足,
∴AF是AE在底面ABCD上的射影,
∴∠EAF就是求AE与下底面所成角的大小,
∴在Rt△EAF中,∠EAF=arctan
因此,AE与下底面所成角的大小为arctan
(2)∵EF//CC'//DD',∴∠AEF就是异面直线AE与DD'所成的角,
∴在Rt△EAF中,∠AEF=arctan
因此,AE与DD'所成角的大小为acrtan
解析
解析已在路上飞奔,马上就到!
知识点
7.如图,已知边长为6的正方形
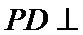
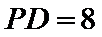
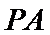
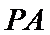
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
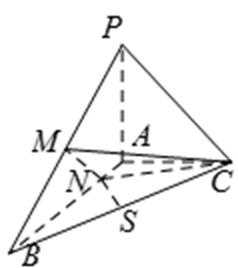
18.已知三棱锥PABC中,PA⊥平面ABC,AB⊥AC,PA=AC=AB,N为AB上一点,AB=4AN,M,S分别为PB,BC的中点.
(1)证明:CM⊥SN;
(2)求SN与平面CMN所成角的大小.
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
15.给出下列命题:
① 已知
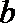
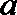
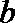
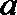

② 在二面角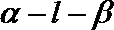
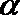
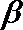
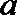
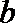
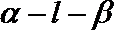
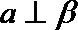
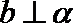
③已知异面直线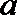
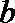
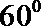
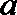
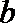
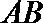
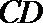
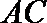
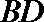
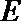
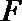
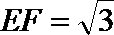
④若正三棱锥的内切球的半径为1,则此正三棱锥的体积最小值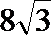
则正确命题的编号是
正确答案
④
解析
解析已在路上飞奔,马上就到!
知识点
19. 如图,在三棱柱










(1)证明:
(2)若


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
17. 设函数
(Ⅰ)判断
(Ⅱ)当


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
19.如图,已知矩形













(1)求证:平面


(2)设





正确答案
(1)证明:
(2)
如图,建立坐标系,则

易知
解析
解析已在路上飞奔,马上就到!
知识点
扫码查看完整答案与解析