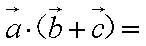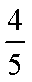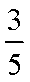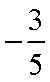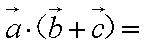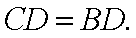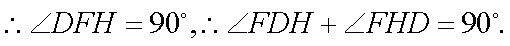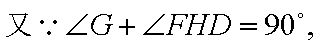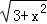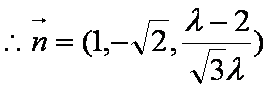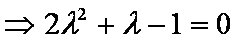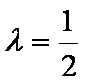- 立体几何与空间向量
- 共2637题
已知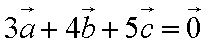
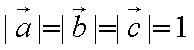
正确答案
解析
向量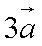
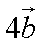
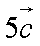
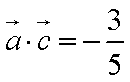
知识点
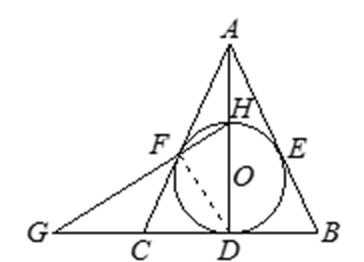
如图,⊙O内切△ABC的边于D、E、F,AB=AC,连接AD交⊙O于点H,直线HF交BC的延长线于点G.
(1)证明:圆心O在直线AD上;
(2)证明:点C是线段GD的中点。
正确答案
见解析。
解析
(1):∵
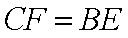
又∵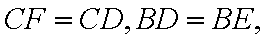
又∵△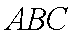
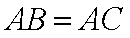
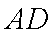
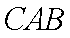
∴内切圆圆心O在直线AD上.(5分)
(2)连接DF,由(1)知,DH是⊙O的直径,
∵圆O与AC相切于点F,
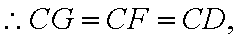
知识点
已知f(x)=m(x﹣2m)(x+m+3),g(x)=2x﹣2,若∀x∈R,f(x)<0或g(x)<0,则m的取值范围是 。
正确答案
(-4,0)
解析
∵g(x)=2x﹣2,当x≥1时,g(x)≥0,
又∵∀x∈R,f(x)<0或g(x)<0
∴此时f(x)=m(x﹣2m)(x+m+3)<0在x≥1时恒成立
则由二次函数的性质可知开口只能向下,且二次函数与x轴交点都在(1,0)的左面
则
∴﹣4<m<0
故答案为:(﹣4,0)
知识点
一个空间几何体的正视图和侧视图都是边长为1的正方形,俯视图是一个直径为1的圆,那么这个几何体的体积为
正确答案
解析
几何体为底面半径为

知识点
已知圆

(1)直线






(2)过圆








正确答案
见解析
解析
(1)①当直线






②若直线


即
设圆心到此直线的距离为

∴

故所求直线方程为
综上所述,所求直线为
(2)设点


则
∵
∴

又∵
由已知,直线m //ox轴,所以,
∴

故轨迹是焦点坐标为

知识点
设平面区域




正确答案
解析
双曲线

抛物线

当直线


知识点
下面的一组图形为某一四棱锥S-ABCD的侧面与底面:
(1)请画出四棱锥S-ABCD的示意图,是否存在一条侧棱垂直于底面?如果存在,请给出证明;如果不存在,请说明理由;
(2)若SA

正确答案
见解析
解析
(1)存在一条侧棱垂直于底面(如图)
证明:


(2)分别取SC、SD的中点G、F,连GE、GF、FA,
则GF//EA,GF=EA,
而由SA

又AD


又SA=AD,F是中点,



知识点
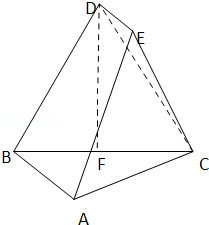
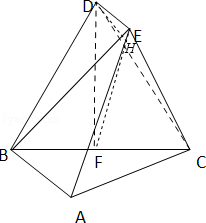
如图,已知多面体ABCDE中,DE⊥平面DBC,DE∥AB,BD=CD=BC=AB=2,F为BC的中点。
(1)求证:DF⊥平面ABC;
(2)求点D到平面EBC的距离的取值范围。
正确答案
见解析
解析
(1)证明:∵DE⊥平面DBC,DE∥AB,∴AB⊥平面DBC,
∵DF⊂平面DBC,∴AB⊥DF
∵BD=CD=BC=2,F为BC的中点
∴DF⊥BC
又∵AB∩BC=B
∴DF⊥平面ABC;
(2)解:设DE=x,连接BE,则x>0
∵DE⊥平面DBC,BC⊂平面DBC,∴DE⊥BC
∵DF⊥BC,DE∩DF=D
∴BC⊥平面DEF
∵BC⊂平面ABC
∴平面DEF⊥平面EBC
连接EF,过D作DH⊥EF,垂足为H,
则DH⊥平面EBC,线段DH的长即为点D到平面EBC的距离
在直角△DEF中,DE=x,DF=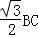
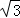
∴DH=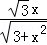
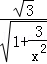
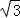
知识点
下图是底面半径为1,母线长均为2的圆锥和圆柱的组合体,则该组合体的侧视图的面积为( )
正确答案
解析

知识点
如图,四棱锥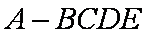
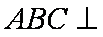
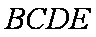

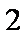
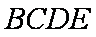

(1)若点
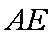
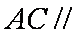

(2)试问点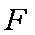
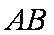
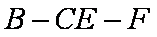

正确答案
见解析
解析
(1)证明:连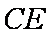
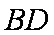
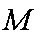
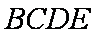
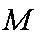
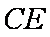
在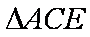

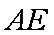
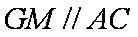
∵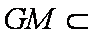
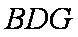
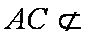

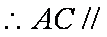
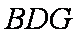
(2)取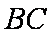
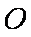
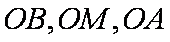
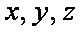
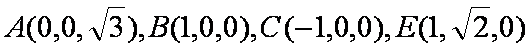
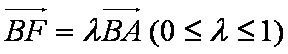
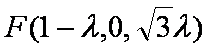
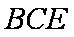
设平面
由
取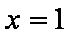
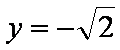
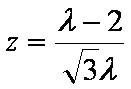
依题意有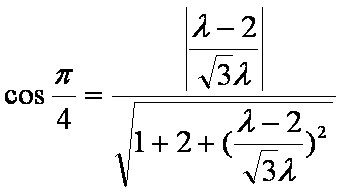
解得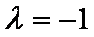
所以当点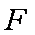
知识点
如图:在四棱锥





(1) 证明:

(2)求三棱锥
(3)在线段PD上是否存在一点E,使得

若存在,求出PE的长;若不存在,说明理由。
正确答案
见解析
解析
证明(1)因为ABCD为菱形,所以AB=BC
又
又M为BC中点,所以
而

又


(2)因为
又


所以,三棱锥

(3)存在
取PD中点E,连结NE,EC,AE,
因为N,E分别为PA,PD中点,所以
又在菱形ABCD中,
所以
所以, 



所以

即在PD上存在一点E,使得

此时
知识点
如图,平面






(1)求证:
(2) 求二面角
正确答案
见解析
解析
解:
(1)证明:连结



故
又因平面

故

于是
又


所以
又因


所以
(2)由(1)得


因为

过



则

在



所以

即二面角

知识点
如图梯形ABCD中
①
③平面DBF

在翻折过程中,可能成立的结论是______。(填写结论序号)
正确答案
②③
解析
考虑①:因为




考虑②:设点





考虑③:当点





考虑④:因为点

知识点
如图,在四棱锥









(1)证明:

(2)当


正确答案
见解析
解析
(1)证明:∵


∴
∵

∴
∴

又∵


∴
又∵
∴

(2)解:∵





又









即直线


知识点
如图所示,



腰三角形,



(1)求证:平面

(2)求直线

正确答案
见解析
解析
(1) 



又


而




(2)连结




由









在






知识点
扫码查看完整答案与解析