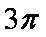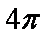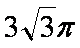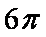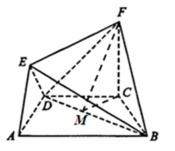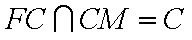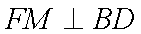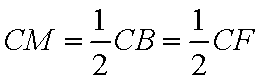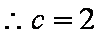- 立体几何与空间向量
- 共2637题
如图，四棱锥P－ABCD的底面是正方形，PA⊥底面ABCD，PA＝2，∠PDA=45，
点E、F分别为棱AB、PD的中点。
（1）求证：AF∥平面PCE；
（2）求三棱锥C－BEP的体积。
正确答案
见解析
解析
解：（1）证明：取PC的中点G，连接GF，因为F为PD的中点，
所以，GF∥CD且
所以，AE∥CD且
所以，AEGF是平行四边形，故AF∥EG，而
（2） 因为PA⊥底面ABCD，所以，PA是三棱锥P-EBC的高，PA⊥AD，PA＝2，
∠PDA=450，所以，AD=2，正方形ABCD中，E为AB的中点，所以，EB=1，故
知识点
已知向量
正确答案
解析
若
知识点
若向量
正确答案
解析
因为
知识点
右图是一个算法的流程图，最后输出的W=
正确答案
解析
开始循环：
再次循环：
再次循环：
知识点
如图，四棱锥E—ABCD中，ABCD是矩形，平面EAB
（1）求证：AE
（2）求三棱锥D—AEC的体积；
（3）求二面角A—CD—E的余弦值。
正确答案
见解析
解析
解析：（1）
（2）
∵AE=EB=2，
（3）以O为原点，分别以OE.OB所在直线为
则
所以二面角A—CD—E的余弦值为
知识点
一个四面体ABCD的所有棱长都为
A
B
C
D
正确答案
解析
显然该四面体是一个正四面体，把这个正四面体置于一个正方体中，在棱长为1的正方体
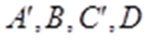
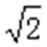
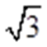
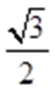
知识点
某三棱锥的三视图如图所示，该三棱锥的体积是（）
A
B4
C2
D
正确答案
解析
由三视图可知：
该三棱锥的侧面PBC⊥底面ABC，PD⊥交线BC，AE⊥BC，且AE=3，PD=2，CD=3，DB=1，CE=EB=2。 所以
知识点
已知直线a和平面
A存在一条直线b，a//b且b
B存在一条直线b，a
C存在一个平面
D存在一个平面
正确答案
解析
A，存在一条直线b，a//b且b
B，存在一条直线b，a
C，存在一个平面
D，存在一个平面
知识点
如图，在四棱锥P—ABCD中，底面ABCD是矩形PA⊥平面ABCD，AP=AB，BP=BC=2，E，F分别是PB,PC的中点。
（1）证明：EF∥平面PAD；
（2）求三棱锥E—ABC的体积V.
正确答案
见解析
解析
（1）在△PBC中，E，F分别是PB，PC的中点，∴EF∥BC.
又BC∥AD,∴EF∥AD,
又∵AD
∴EF∥平面PAD.
（2）连接AE,AC,EC,过E作EG∥PA交AB于点G,
则EG⊥平面ABCD,且EG=
在△PAB中，AD=AB,
∴S△ABC=
∴VE-ABC=
另解：
知识点
若某空间几何体的三视图如图所示，则该几何体的表面积是
A
B
C
D
正确答案
解析
由三视图知：该几何体为三棱柱，三棱柱的底面为直角三角形，两直角边分别为1和
知识点
在如图所示的几何体中，四边形ABCD是等腰梯形，AB∥CD，∠DAB= 60°，FC⊥平面ABCD，AE⊥BD，CB= CD= CF。
（1）求证：BD⊥平面AED；
（2）求二面角F—BD—C的正切值。
正确答案
见解析。
解析
（1）在等腰梯形ABCD 中，AB ∥CD ，∠DAB=60 °，CB=CD ，
由余弦定理可知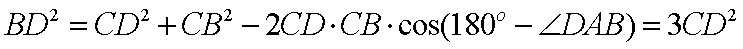
即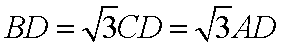
在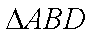
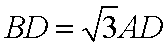
则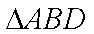
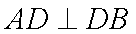
又AE⊥BD，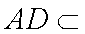
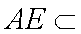
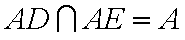
故BD⊥平面AED………………6分
（2）过C作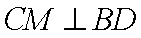
因为FC⊥平面ABCD，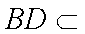
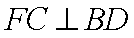
所以BD⊥平面FCM.
因此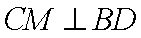
故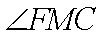
在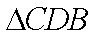
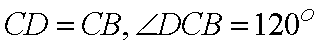
因此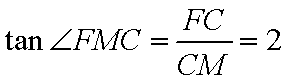
知识点
若直线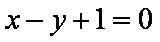
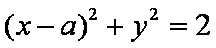
A[－3，－1]
B[－1，3]
C[－3,l ]
D（－∞，－3] 
正确答案
解析
因为直线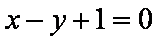
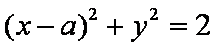
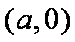
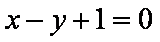
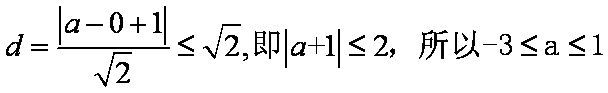
知识点
一个空间几何体的三视图如图所示，则该几何体的表面积为
A48
B32十
C48 +
D 80
正确答案
解析
由三视图知：该几何体为侧视图为底的直四棱柱，其底面上底长2，下底长为4，高为4 的等腰梯形，且等腰梯形的腰长为
知识点
已知向量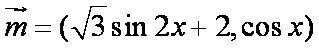
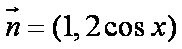
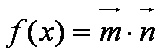
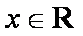
（1）求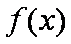
（2）在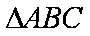
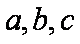
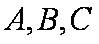
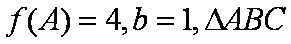
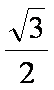
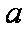
正确答案
见解析
解析
解：（1）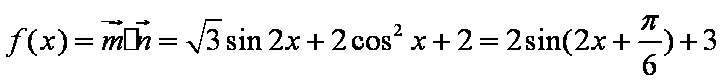
∴
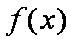
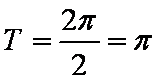
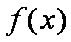
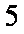
（2）由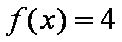
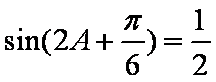
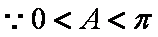
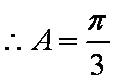
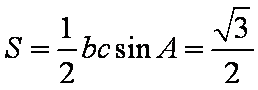
由余弦定理得：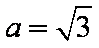
知识点
如图ACB=90°，CD⊥AB于点D，以BD为直径的圆与BC交于点E，下面的结论正确的是 。
①CE·CB=AD·DB;
②CE·CB=AD·AB;
③AD·AB=CD2
正确答案
①
解析
在
知识点
扫码查看完整答案与解析