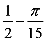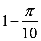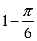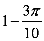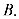- 立体几何与空间向量
- 共2637题
14.正四面体



正确答案
解析
将四面体ABCD放置于正方体中,如图所示
可得正方体的外接球就是四面体ABCD的外接球,
∵正四面体ABCD的棱长为4,
∴正方体的棱长为
可得外接球半径R满足2R=
E为棱BC的中点,过E作其外接球的截面,当截面到球心O的距离最大时,
截面圆的面积达最小值,
此时球心O到截面的距离等于正方体棱长的一半,
可得截面圆的半径为r=
得到截面圆的面积最小值为S=
故答案为:4π
知识点
5.已知某几何体的三视图(单位:cm)如图所示,则该几何体的体积是( )
正确答案
解析
如图所示,原几何体为:
一个长宽高分别为6,3,6的长方体砍去一个三棱锥,底面为直角边分别为3,4直角三角形,高为4.因此该几何体的体积=3×6×6﹣
知识点
5.已知圆锥的母线长为
正确答案
解析





知识点
19.在长方体






(1) 求几何体

(2)求异面直线

正确答案
见解析。
解析
(1)


左视图如下图所示.
(2)依据题意,有

∴


又
∴
∴异面直线


知识点
13.已知直线






正确答案
±2
解析
因为向量

【思路点拨】本题先由向量加法与减法的几何意义得到OA⊥OB,再由所给直线与圆的特殊性确定实数a的值.
知识点
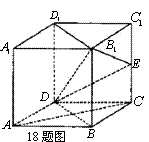
18.如图,已知四棱柱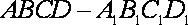
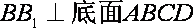
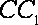
(1)求证:
(2)求证:AC∥平面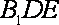
正确答案
见解析。
解析
(1)因为底面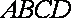

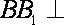
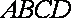
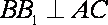
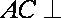
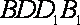
(2)设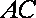
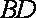
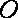
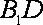

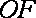
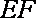
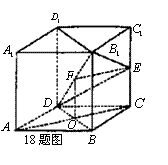
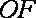
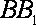
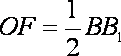
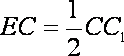
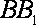
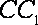
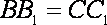
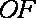
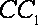
且
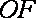
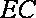
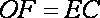
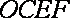
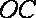
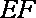
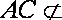
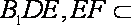
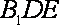
所以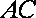
知识点
10.某同学为了研究函数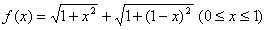
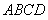
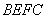
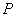
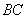
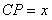
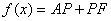
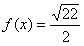
正确答案
解析
从图中知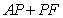
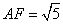
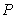
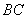
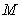
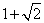
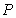
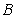
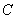
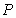
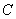
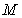
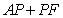
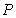
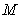
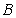
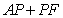
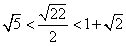
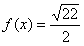
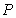
知识点
13.已知

正确答案
解析
∵

∴

知识点
4.执行如图所示程序框图所表达的算法,若输出的x值为48,则输入的x值为( )
正确答案
解析
x←2x,n=1+1=2,满足n≤3,执行循环体;
x=2×(2x)=4x,n=2+1=3,满足n≤3,执行循环体;
x=2×(4x)=8x,n=3+1=4,不满足n≤3,退出循环体,
由8x=48即可得x=6.
则输入的x值为:6.
故选B.
知识点
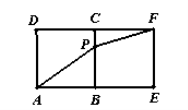
6.一只受伤的丹顶鹤在如图所示(直角梯形)的草原上飞过其中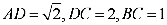
正确答案
解析
过点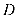
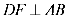
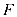
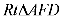
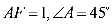
梯形的面积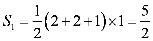
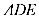
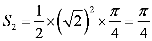
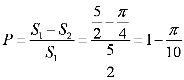
知识点
21.如下图,AB、CD是圆的两条平行弦,BE//AC,BE交CD于E、交圆于F,过A点的切线交DC的延长线于P,PC=ED=1,PA=2.
(1)求AC的长;
(2)求证:BE = EF.
正确答案
见解析。
解析
(1)

又



(2)




知识点
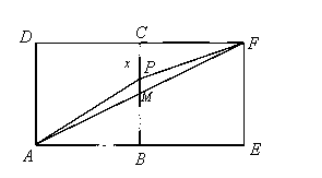
21.有一块铁皮零件,其形状是由边长为











(1)试求出矩形铁皮


(2)试问如何截取(即

正确答案
见解析。
解析
解析:(1)依据题意并结合图形,可知:
1 当点



2 当点




于是,
所以,

(2)由(1)知,当

当


因此,

所以,先在












知识点
14.一个平面图由若干顶点与边组成,各顶点用一串从1开始的连续自然数进行编号,记各边的编号为它的两个端点的编号差的绝对值,若各条边的编号正好也是一串从1开始的连续自然数,则称这样的图形为“优美图”.已知如图是“优美图”,则点A,B与边a所对应的三个数分别为________.
正确答案
3、6、3
解析
观察图中编号为4的边,由于6-2=5-1=4,而数字2已为一端点的编号,故编号为4的边的左、右两端点应为5、1,从而易知编号为1的边的左、右两端点应为4、3.考虑到图中编号为1的边,易知点A对应的数为3,点B对应的数为6.故应填3、6、3.
知识点
11.一个几何体的三视图如图所示,则该几何体的体积是()
正确答案
12
解析
该几何体是两个全等的斜四棱柱对接而成的几何体,其中每个四棱柱是底面邻边长分别为3, 2的长方形,高为1,所以该几何体的体积为:
知识点
17.如图,已知PA⊥平面ABCD,且四边形ABCD为矩形,M,N分别是AB,PC的中点.
(1)求证:MN⊥CD;
(2)若∠PDA=45°,求证:MN⊥平面PCD.
正确答案
见解析。
解析
(1)
如图所示,取PD的中点E,连接AE,NE,
∵N是PC的中点,E为PD的中点,
∴NE∥CD,且NE=
而AM∥CD,且AM=

∴NE綊AM,
∴四边形AMNE为平行四边形,
∴MN∥AE.
又PA⊥平面ABCD,∴PA⊥CD,
又∵ABCD为矩形,∴AD⊥CD.
而AD∩PA=A,∴CD⊥平面PAD,
∴CD⊥AE.又AE∥MN,∴MN⊥CD.
(2)∵PA⊥平面ABCD,∴PA⊥AD,
又∠PDA=45°,
∴△PAD为等腰直角三角形.
又E为PD的中点,
∴AE⊥PD,又由(1)知CD⊥AE,PD∩CD=D,
∴AE⊥平面PCD.
又AE∥MN,∴MN⊥平面PCD.
知识点
扫码查看完整答案与解析