- 立体几何与空间向量
- 共2637题
9.已知





正确答案
解析
解析已在路上飞奔,马上就到!
知识点
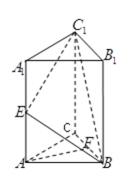
20.如图所示,在四棱锥


(1)求证:
(2)求证:平面PDC
(3)求四棱锥
正确答案
(1)
连接EF,AC
∵四棱锥
∴对角线AC经过F点
又在
∴EF为
∴
又
∴
(2)∵底面ABCD是边长为a的正方形
∴
又侧面


∴
又
∴平面PDC
(3)过点P作AD的垂线PG,垂足为点G
∵侧面


∴

又
∴
∴
解析
解析已在路上飞奔,马上就到!
知识点
4.如图,矩形长为6,宽为2,在矩形内随机地撒300颗黄豆,数得落在椭圆外的黄豆数为96颗,以此实验数据为依据可以估算出椭圆的面积约为( )
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
5.已知

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
20.已知椭圆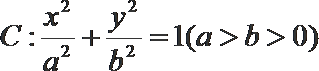
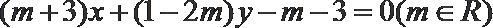
(1)求椭圆
(2)若直线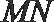
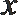
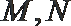

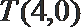
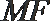
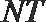
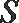
①求证:点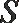

②求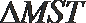
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
20. 已知三棱柱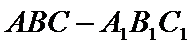
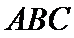
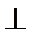


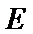

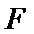
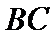
(Ⅰ)求证:直线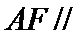

(Ⅱ)求点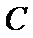

正确答案
(Ⅰ)取

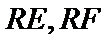
则
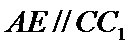

所以四边形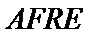
则


(Ⅱ)由等体积法得
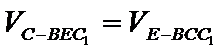
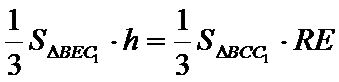
得
解析
解析已在路上飞奔,马上就到!
知识点
17.已知向量
(1)求
(2)将函数





正确答案
解析
解析已在路上飞奔,马上就到!
知识点
5.已知向量


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
7. 某几何体的三视图如图所示,它的体积为( )
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
9.平面向量





正确答案
解析
解析已在路上飞奔,马上就到!
知识点
10.若一个底面是正三角形的三棱柱的正视图如图所示,其侧视图面积等于( )
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
14.已知





正确答案
解析
解析已在路上飞奔,马上就到!
知识点
18.已知

(Ⅰ)求


(Ⅱ)求
正确答案
(Ⅰ)
∴
∵
∴
(Ⅱ)∵
∴
解析
解析已在路上飞奔,马上就到!
知识点
2.已知某个几何体的三视图如下图,根据图中标出的尺寸(单位:cm),可得这个几何体的体积是( )
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
20. 如图,四面体


(I)求证:
(II)试问该四面体的体积是否存在最大值?若存在,求出这个最大值及此时棱长
正确答案
(Ⅰ)
证明 取


∵

∴

又∵
∴



∴
(Ⅱ)解:由已知得,

设







当


∴该四面体存在最大值,最大值为8,
此时棱长
解析
解析已在路上飞奔,马上就到!
知识点
扫码查看完整答案与解析