- 立体几何与空间向量
- 共2637题
18．如图所示，在四棱锥PABCD中，AB⊥平面PAD，AB∥CD，PD＝AD，E是PB的中点，F是DC上的点且DF＝
（1）证明：PH⊥平面ABCD；
（2）若PH＝1，AD＝
正确答案
（1）证明：由于AB⊥平面PAD，
PH
又∵PH为△PAD中AD边上的高，
∴ AD⊥PH．
∵ AB∩AD＝A，AB
AD
∴ PH⊥平面ABCD．
（2）由于PH⊥平面ABCD，
E为PB的中点，PH＝1，
故E到平面ABCD的距离h＝
又∵ AB∥CD，AB⊥AD，∴ AD⊥CD，
故S△BCF＝
因此VEBCF
＝
＝
解析
解析已在路上飞奔，马上就到！
知识点
17．如图，在四棱柱ABCD-
平面
（Ⅰ）
（Ⅱ）
（Ⅲ） 若
正确答案
（Ⅰ）证：在四棱锥
取
又
面
（Ⅱ）连
在正
又在正
∴
又
在四棱锥中， 
∴
又
∴面
又
（Ⅲ）过
连
所以
由已知得：
解析
解析已在路上飞奔，马上就到！
知识点
10．图是某几何体的三视图，则该几何体的体积等于（ ）
A
B
C1
D
正确答案
解析
解析已在路上飞奔，马上就到！
知识点
16．在三棱锥P-ABC中，PB=6，AC=3，G为△PAC的重心，过点G作三棱锥的一个截面，使截面平行于直线PB和AC，则截面的周长为（ ）．
正确答案
8
解析
解析已在路上飞奔，马上就到！
知识点
11．已知向量
正确答案
解析
解析已在路上飞奔，马上就到！
知识点
19．如图，五面体中，四边形ABCD是矩形，DA
（I）求证：PQ//平面BCE；
（II）求证：AM
正确答案
解析
解析已在路上飞奔，马上就到！
知识点
10．几何体的三视图如图所示，则这个几何体的直观图可以是（ ）
A
B
C
D
正确答案
解析
解析已在路上飞奔，马上就到！
知识点
3．已知非零向量
A
B
C
D
正确答案
解析
解析已在路上飞奔，马上就到！
知识点
2．若向量
正确答案
解析
解析已在路上飞奔，马上就到！
知识点
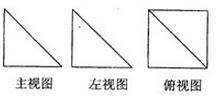
9．一个几何体的三视图如图所示，其中主视图和左视图是腰长为4的两个全等的等腰直角三角形，若该几何体的所有顶点在同一球面上，则该球的表面积是（ ）
A
B
C
D
正确答案
解析
解析已在路上飞奔，马上就到！
知识点
5．如图是一个几何体的三视图，则该几何体的体积为（ ）
A2
B
C
D
正确答案
解析
解析已在路上飞奔，马上就到！
知识点
17． 如图，在四棱锥
（Ⅰ）求证：
（Ⅱ）求证：
（Ⅲ）求四棱锥
正确答案
（Ⅰ）证明：设
在
又
（Ⅱ）证明：
又
（Ⅲ）答案：
在
在
解析
解析已在路上飞奔，马上就到！
知识点
8．△PAB所在的平面α和四边形ABCD所在的平面β垂直，且AD⊥α，BC⊥α，AD=4，BC=8，AB=6，∠APD=∠CPB，则点P在平面α内的轨迹是（ ）
正确答案
解析
解析已在路上飞奔，马上就到！
知识点
9．已知向量
正确答案
解析
解析已在路上飞奔，马上就到！
知识点
6．已知向量
A
B
C
D4
正确答案
解析
解析已在路上飞奔，马上就到！
知识点
扫码查看完整答案与解析