- 立体几何与空间向量
- 共2637题
15．给定两个长度为1的平面向量
正确答案
2
解析
解析已在路上飞奔，马上就到！
知识点
12．平面向量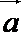
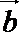
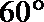
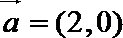
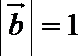
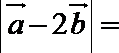
正确答案
2
解析
解析已在路上飞奔，马上就到！
知识点
15．已知
正确答案
4
解析
解析已在路上飞奔，马上就到！
知识点
19．如图所示，四棱锥P-ABCD中，底面ABCD是边长为2的菱形，Q是棱
（Ⅰ）若Q是PA的中点，求证：PC//平面BDQ；
（Ⅱ）若PB=PD，求证：BD⊥CQ；
（Ⅲ）在（Ⅱ）的条件下，若PA=PC，PB=3，
∠ABC=60º，求四棱锥P-ABCD的体积．
正确答案
（Ⅰ）连结AC，交BD于O．
因为 底面ABCD为菱形，
所以 O为AC中点．
因为 Q是PA的中点，
所以 OQ// PC，
因为OQ
所以PC//平面BDQ．
（Ⅱ）因为 底面ABCD为菱形，
所以 AC⊥BD，O为BD中点．
因为 PB=PD，
所以 PO⊥BD．
因为 PO∩BD =O，
所以 BD ⊥平面PAC．因为 CQ
所以 BD⊥CQ．
（Ⅲ）因为 PA=PC，
所以 △PAC为等腰三角形 ．
因为 O为AC中点，
所以 PO⊥AC．
由（Ⅱ）知 PO⊥BD，且AC∩BD =O，
所以 PO⊥平面ABCD，即PO为四棱锥P-ABCD的高．
因为四边形是边长为2的菱形，且∠ABC=60º，
所以BO=
所以PO=
所以 
解析
解析已在路上飞奔，马上就到！
知识点
11．若
A
B
C
D不存在
正确答案
解析
解析已在路上飞奔，马上就到！
知识点
18．如图，在底面是矩形的四棱锥
（1）求证：平面
（2）求三棱锥
正确答案
（1）略；
（2）
解析
解析已在路上飞奔，马上就到！
知识点
2． 已知向量
A
B
C
D0
正确答案
解析
解析已在路上飞奔，马上就到！
知识点
19．在如图所示的组合体中，三棱柱
（Ⅰ）若圆柱的轴截面是正方形，当点
（Ⅱ）当点
正确答案
（Ⅰ）
（Ⅱ）设圆柱的底面半径为
当点
∴
解析
解析已在路上飞奔，马上就到！
知识点
7.在边长为1的菱形ABCD中，∠ABC=60O，将菱形沿对角线AC折起，使折起后BD=1，则三棱锥B-ACD的体积为（ ）
A
B
C
D
正确答案
解析
解析已在路上飞奔，马上就到！
知识点
8. 某几何体的主视图与俯视图如图所示，左视图与主视图相同，且图中的四边形都是 边长为2的正方形，两条虚线互相垂直，则该几何体的体积是( )
A
B
C
D
正确答案
解析
解析已在路上飞奔，马上就到！
知识点
5．若
A
B
C
D
正确答案
解析
解析已在路上飞奔，马上就到！
知识点
5．将圆锥的侧面展开后得到一个半径为
正确答案
解析
解析已在路上飞奔，马上就到！
知识点
6．已知某个几何体的三视图如图（主视图中的弧线是半圆），根据图中标出的尺寸（单位：
正确答案
解析
解析已在路上飞奔，马上就到！
知识点
11．定义
正确答案
（1，2009）
解析
解析已在路上飞奔，马上就到！
知识点
20．如图：
（1）求
（2）求异面直线
正确答案
（1）由题知：
则△
则
则
（2）因为
则
即有
所以
在直角三角形
所以直线
解析
略
知识点
扫码查看完整答案与解析