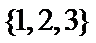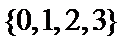- 立体几何与空间向量
- 共2637题
14.已知




正确答案
解析
解析已在路上飞奔,马上就到!
知识点
18. 如图,三角形









(Ⅰ)求证:

(Ⅱ)求几何体
正确答案
(I)
解:取


因为


所以

又因为
所以

所以




所以平面

所以

(II)取




又平面



所以

因为三角形
所以
因为


解析
解析已在路上飞奔,马上就到!
知识点
8.如图,水平放置的正三棱柱
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
1.若集合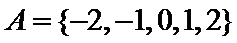
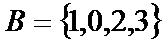
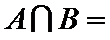
正确答案
解析



而集合


知识点
6.一个几何体的三视图如图所示,则该几何体外接球的表面积为( )
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
3.一个几何体的三视图如图所示,其中正视图是一个正三角形,则该几何体的外接球的表面积为( )
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
15.已知向量







正确答案
解析
解析已在路上飞奔,马上就到!
知识点
19. 在直三棱柱




(1)求证:
(2)若




正确答案
(1)证明:



又






又 









(2)在直三棱柱







在



在
由(1)知





解析
解析已在路上飞奔,马上就到!
知识点
6.已知向量




正确答案
解析
解析已在路上飞奔,马上就到!
知识点
8.某几何体的三视图如图1所示,且该几何体的体积是

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
19.如图,在四棱锥




(1)若


(2)点





正确答案
解:
(1)连





又
(2)当

连






又




令菱形








解析
解析已在路上飞奔,马上就到!
知识点
12.如图所示,在平行四边形





正确答案
解析
解析已在路上飞奔,马上就到!
知识点
18. 在如图所示的几何体中,平面






(Ⅰ)求证:

(Ⅱ)求三棱锥
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
8.设有一几何体的三视图如下,则该几何体体积为( )
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
8.三棱锥S-ABC及其三视图中的正视图和侧视图如图所示,则棱SB的长为( )
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
扫码查看完整答案与解析