立体几何与空间向量_章节学习

1

题型：单选题

|

单选题 · 5 分

5. 已知向量，，若，则（）

A1

B

C

D

正确答案

C

解析

解析已在路上飞奔，马上就到！

知识点

空间几何体的结构特征

1

题型：单选题

|

单选题 · 5 分

11．若，则的取值范围为（）

A

B

C

D

正确答案

D

解析

解析已在路上飞奔，马上就到！

知识点

空间几何体的结构特征

1

题型：填空题

|

填空题 · 5 分

14．若圆锥的内切球与外接球的球心重合，且内切球的半径为，则圆锥的体积为___________。

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

空间几何体的结构特征

1

题型：单选题

|

单选题 · 5 分

6．已知某几何体的三视图，则该几何体的体积是（）

A12

B24

C36

D48

正确答案

A

解析

解析已在路上飞奔，马上就到！

知识点

空间几何体的结构特征

1

题型：简答题

|

简答题 · 12 分

18.如图, 是边长为的正方形，平面，，.

（1）求证：平面；

（2）设点是线段上一个动点，试确定点的位置，使得平面，并证明你的结论.

正确答案

（1）证明：因为平面，

所以.

因为是正方形，

所以，因为

从而平面.

（2）当M是BD的一个三等分点，即3BM＝BD时，AM∥平面BEF．

取BE上的三等分点N，使3BN＝BE，连结MN，NF，则DE∥MN，且DE＝3MN，

因为AF∥DE，且DE＝3AF，所以AF∥MN，且AF＝MN，

故四边形AMNF是平行四边形．

所以AM∥FN，

因为AM平面BEF，FN平面BEF，

所以AM∥平面BEF．

解析

解析已在路上飞奔，马上就到！

知识点

空间几何体的结构特征

1

题型：简答题

|

简答题 · 12 分

18．在如图所示的几何体中，四边形为矩形，平面平面，，，，，点在棱上．

（Ⅰ）若为的中点，求证：//平面；

（Ⅱ）若直线与平面所成角的正弦值为，求的长度．

正确答案

解：

（Ⅰ）证明：连接BD，交AC于点O，连接OP．

因为P是DF中点，O为矩形ABCD 对角线的交点，

所以OP为三角形BDF中位线，

所以BF // OP，

因为BF平面ACP，OP平面ACP，

所以BF // 平面ACP．

（Ⅱ）因为∠BAF=90º，所以AF⊥AB，

又因为平面ABEF⊥平面ABCD，

且平面ABEF ∩平面ABCD= AB，

所以AF⊥平面ABCD

从而AF⊥CD

又因为四边形ABCD为矩形

所以AD⊥CD

从而CD⊥平面FAD

所以∠CPD就是直线PC与平面FAD所成的角

又且

解析

解析已在路上飞奔，马上就到！

知识点

空间几何体的结构特征

1

题型：单选题

|

单选题 · 5 分

10．设向量，，定义一种向量积：．已知向量，，点P在的图象上运动，点Q在的图象上运动，且满足（其中O为坐标原点），则在区间上的最大值是（）

A4

B2

C

D

正确答案

A

解析

解析已在路上飞奔，马上就到！

知识点

空间几何体的结构特征

1

题型：简答题

|

简答题 · 12 分

18．一个四棱锥的三视图和直观图如图所示，其中俯视图中．E为侧棱PD的中点．

（1）求证：PB//平面AEC；

（2）若F为侧棱PA上的一点，且，则为何值时，PA平面BDF？并求此时几何体F—BDC的体积．

正确答案

（1）由图形可知该四棱锥和底面ABCD是菱形，且有一角为，边长为2，锥体高度为1。

设AC，BD和交点为O，连OE，OE为△DPB的中位线，

OE//PB，EO面EAC，PB面EAC内，PB//面AEC

（2）过O作OFPA垂足为F

在Rt△POA中，PO=1，AO=，PA=2，PO2=PF·PA，2PF=1

在棱形中BDAC，又因为PO面ABCD，所以BDPO，

及BD面APO，所以PA平面BDF

当时，在△POA中过F作FH//PO，则FH面BCD，FH=

。

解析

解析已在路上飞奔，马上就到！

知识点

空间几何体的结构特征

1

题型：简答题

|

简答题 · 13 分

19.如图，在多面体中，四边形是正方形，是等边三角形，。

（1）求证：；

（2）求多面体的体积。

正确答案

证明及解：

（1）取中点，连，

∥

∥，∥

四边形是平行四边形

∥，∥

又平面，平面

∥平面

在正方形中，∥，∥，

四边形为平行四边形

∥

又平面，平面

∥平面

，平面∥平面

又平面

∥平面．

（2）在正方形中，

又是等边三角形，所以，

所以

于是

又，平面，

又，平面

于是多面体是由直三棱柱和四棱锥组成的．

又直三棱柱的体积为，

四棱锥的体积为，

故多面体的体积为．

解析

解析已在路上飞奔，马上就到！

知识点

空间几何体的结构特征

1

题型：单选题

|

单选题 · 5 分

5．在棱长为1的正方体中，二面角的正切值是（）

A

B

C

D

正确答案

A

解析

解析已在路上飞奔，马上就到！

知识点

空间几何体的结构特征

1

题型：简答题

|

简答题 · 12 分

19．在四棱锥中，平面，底面为直角梯形，∥，，,。

（Ⅰ）求异面直线与所成角的大小；

（Ⅱ）求直线与平面所成角的正弦值。

正确答案

解一：（Ⅰ）直角梯形中∥异面直线所成的角就是所成的角（或其补角）。连结

由已知有

所以是等腰直角三角形，所以

故异面直线与所成角为

（Ⅱ）由已知有

直角梯形中

设到平面的距离为，由

由（Ⅰ）知；设与平面所成角为，则有

解法二：以为原点，为轴建立坐标系

（Ⅰ）

（Ⅱ）可求得平面的一个法向量为，设与平面所成角为，

有

解析

解析已在路上飞奔，马上就到！

知识点

空间几何体的结构特征

1

题型：简答题

|

简答题 · 13 分

20．在xoy平面上有一点列，点位于曲线（）上，以点为圆心的⊙与X轴都相切，且⊙与⊙又彼此外切，若，且（）。

（1）求证：数列是等差数列；

（2）设⊙的面积为，，求。

正确答案

解：（1）∵以点为圆心的⊙与X轴都相切，

∴⊙的半径

又∵⊙与⊙彼此外切，∴|⊙⊙|

∴

即

∵，∴

∴是以为首项，公差为2的等差数列。

（2）由（1）得

又

∴

解析

解析已在路上飞奔，马上就到！

知识点

空间几何体的结构特征

1

题型：简答题

|

简答题 · 13 分

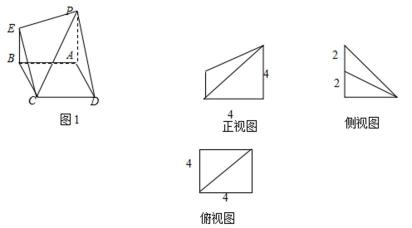
18.图1是一几何体的直观图，右图是该几何体的三视图。

（I）若F为PD的中点，求证AF⊥平面PCD；

（II）求几何体BCE—APD的体积；

（III）若PB和AE交于G点，求四棱锥G—ABCD的体积。

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

空间几何体的结构特征

1

题型：单选题

|

单选题 · 5 分

5．一组数据3，4，5，s，t的平均数是4，中位数是m，则过点和的直线与直线的位置关系是（）

A平行

B相交但不垂直

C重合

D垂直

正确答案

D

解析

解析已在路上飞奔，马上就到！

知识点

空间几何体的结构特征

1

题型：单选题

|

单选题 · 5 分

9.给定两个模为1的平面向量和，它们的夹角为，如图，点C在以O为圆心的圆弧AB上运动，若，其中，则的最大值是（）

A1

B2

C

D

正确答案

D

解析

解析已在路上飞奔，马上就到！

知识点

空间几何体的结构特征

热门试卷

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点